Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 1
Três tábuas, cada uma com seção transversal retangular de 40 x 90 mm, são pregadas juntas para formar uma viga que é submetida a uma força cortante vertical de 1,1 kN. Sabendo-se que o espaçamento entre cada um dos pares de pregos é de 60 mm, determinar a força cortante em cada prego.
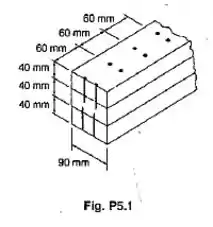
Passo 1
Do enunciado temos que a cortante vertical é de 1,1 kN.
Nosso momento de inércia será dado por
Vamos ter para a área da seção de uma dessas tábuas
Adistancia entre a linha neutra e o centro dessa área é
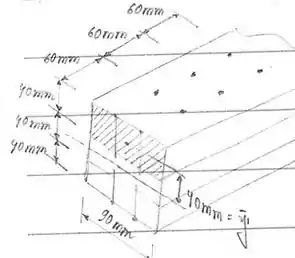
Passo 2
Temos ainda para Q
Então o é dado por
Para cada prego teremos então
Observe que estamos multiplicando por 2 por termos 2 pregos por fileira.
Resposta
Exercícios de Livros Relacionados
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine o espaçamento máximo s para os parafusos se cada um deles puder resistir a um cisalhamento de20k N e o cisalhamento apl
A viga está sujeita a um cisalhamento V = 800N . Determine a tensão de cisalhamento média desenvolvida nos pregos ao longo dos lados A e B se eles estiverem espaçados de s = 100 m m . Cada prego tem d
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150m m e espessura de 12m m . Se os parafusos estiverem espaçados de s = 200 m m , determine a força de c
A viga-mestra de alma dupla é composta por duas chapas de compensado presas a elementos de madeira na parte superior e na parte inferior. Se cada elemento de fixação puder suportar 3k N em cisalhament
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150m m e espessura de 12m m . Se um cisalhamento V = 250k N for aplicado à seção transversal, determine o