Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 119
Resolver o Prob. 55.117, quando , , e .
Passo 1
Temos a seguinte situação:
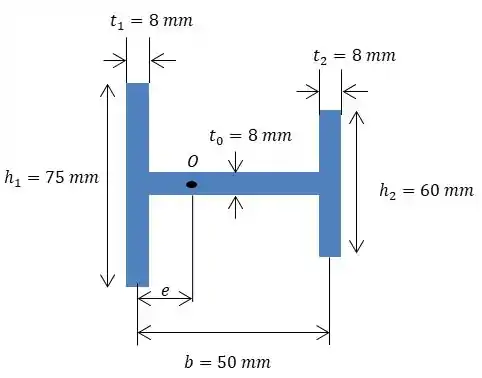
Nosso objetivo é determinar a localização do centro de cisalhamento da viga de parede fina.
Para calcular isto, vamos integrar o fluxo de cisalhamento sobre a viga para determinar a forças internas. Após isto, vamos fazer o cálculo do momento equivalente para determinar distância .
Vamos determinar apenas trabalhando com aba direita menor.
Passo 2
Começando com o cálculo do momento de inércia.
Possuímos retângulos e não consideremos o momento de inércia da viga central. Pois, o momento de inércia deste retângulo com relação ao eixo é muito pequeno para ser considerado.
Por definição temos o momento de inércia:
Passo 3
Vamos determinar a força na aba menor.
Em que a tensão cisalhante média é:
Temos que determinar nosso momento estático para dar continuidade, sobre a força cisalhante fique tranquilo que ira ser simplificada.
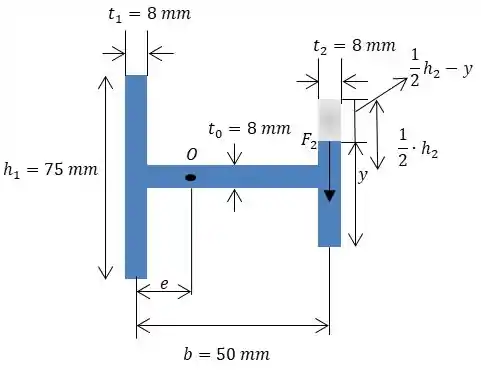
Determinando o momento estático:
Precisamos determinar a área da aba:
Determinando o centroide da nossa aba:
Efetuando a multiplicação:
Passo 4
Agora que temos o momento de inércia estático, podemos determinar :
Para determinar , vamos deixar claro nossa tensão cisalhante.
Substituindo o momento estático:
Temos que é definido por:
Simplificando e inserindo os limites de integração para a variável
Vamos considerar o meio da viga como coordenada zero, logo, teremos indo de até
Substituindo na integral:
Aplicando os limites de integração:
Por final, vamos substituir o momento de inércia:
Passo 5
Como temos podemos executar o cálculo do momento equivalente para determinara distância .
Considerando sentido anti-horário positivo.
Simplificando e isolando :
Ta ai!! Basta substituirmos os valores, vamos ignorar este negativo, pois é uma unidade de comprimento, o que é compreensível fazer está aproximação:
Deixarei as unidades em milímetros para termos uma ideia melhor de dimensão no desenho da viga.