Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 131
Para perfil e o carregamento do Prob. 5.130, determinar a distribuição de tensões de cisalhamento ao longo da linha perna vertical.
Passo 1
Iremos deduzir a fórmula de cisalhamento para a linha em função de , para qualquer valor de teremos um resultado diferente para tal.
Primeiramente vamos decompor o vetor , para entendermos atuação da carga.
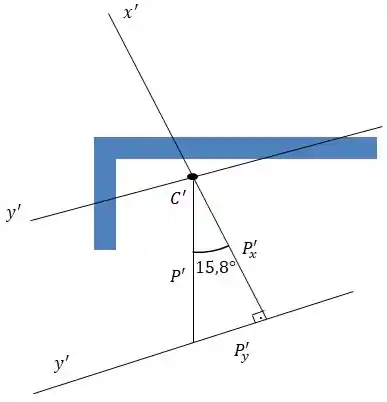
Reescrevi o eixo parcial para que ficasse mais fácil de encher o triângulo retângulo.
Aplicando trigonometria, temos:
Para outra componente:
Negativo, pois o sentido é contrária a tensão cisalhante.
Passo 2
Temos que determinar agora as coordenadas dos centroides dos nossos eixos superpostos, e .
Para isto, segue um desenho para ajudar:
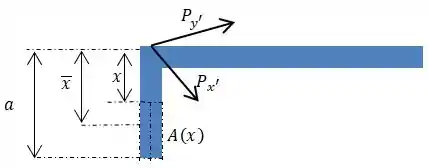
Com isto teremos as seguintes coordenadas:
e
Mas perceba que estas coordenadas que determinamos aqui não são referentes aos eixos . Portanto, vamos transformar estas coordenadas:
E para centroides:
Substituindo , e simplificando ao máximo:
Substituindo
Para coordenada :
Substituindo , e simplificando ao máximo:
Substituindo
Passo 3
Agora que temos todas as coordenadas, podemos determinar a tensão de cisalhamento na linha .
A tensão máxima será a soma da tensão de cisalhamento das duas coordenadas.
Substituindo nossos cálculos anteriores:
Para qualquer valor de a ou teremos a tensão cisalhante distribuída na marra
Resposta
Para qualquer valor de a ou teremos a tensão cisalhante distribuída na marra