Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 33

Resolver o Prob. 5.32, considerando que a dimensão t é aumentada para 7,6mm.

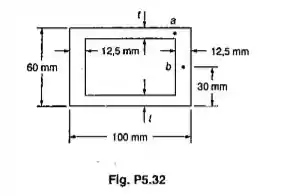
Passo 1

Precisamos calcular o momento de inércia:

I =   100 × 60 3 12 - 100 - 25 × 60 - 15,2 3 12 = 1 , 24 × 10 6 m m 4

Vamos agora calcular o momento estático para encontrar a tensão no ponto A. Lembrando que nesses casos é sempre bom pensar no fluxo de cisalhamento, que se divide em partes iguais se o trecho for simétrico. Então vamos criar um ponto a’ que seja simétrico ao ponto a e separar esse trecho da viga.

O momento estático do trecho para o ponto A será:

Q a = y - A = 30 - 7,6 / 2 × 100 - 25 × 7,6 = 14,934 × 10 3 m m ³

Passo 2

Com isso o fluxo de cisalhamento no trecho é:

q 1 = V Q I t o t a l = 45 × 10 3 × 1 4,934 × 10 3 1 , 24 × 10 6

q 1 = 541,96 N / m m

Porém como dito antes, o fluxo se divide de forma igual para a e a’, assim:

q a = q 1 2 = 2 70,98 N / m m

A tensão de cisalhamento será então:

τ a = q a t = 2 70,98 7,6 = 3 5,66 M p a

Passo 3

Vamos agora calcular o momento estático para encontrar a tensão no ponto B. Perceba que o ponto B se encontra exatamente no meio da seção transversal, nesse caso é legal desenhar uma linha horizontal e separar a seção em dois trechos.

Com isso podemos calcular o momento estático:

Q b = ∑ y - A = 30 - 7,6 2 × 100 - 25 × 7,6 + 2 × ( 12,5 × 30 × 15 ) = 2 6,184 × 10 3 m m ³

E com isso o fluxo de cisalhamento será:

q = V Q I t o t a l = 45 × 10 3 × 2 6,184 × 10 3 1 , 24 × 10 6 = 950,228 N / m m

Passo 4

Como desenhado na figura, a linha horizontal corta B e B’, isso mostra que o fluxo de cisalhamento naquele ponto é dividido por 2.

q b = q 2 = 475 , 114 N / m m

E enfim a tensão:

τ b = q b t = 475 , 114 12,5 = 38 , 001 M p a

Resposta

  1. τ a = 3 5 , 6 6 M P a
  2. τ b = 38,001 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Selecione no Apêndice B a viga com avanço de abas largas de aço que tenha o menor peso e que suportará com segurança as cargas. Considere que o apoio em A é um pino e que o apoio em B é um rolete. A t
Os mancais em A e B exercem somente as componentes x e z das forças sobre o eixo de aço. Determine, com aproximação de 1m m , o diâmetro do eixo, de modo que ele possa resistir às cargas das engrenage
Faça um rascunho da intensidade da distribuição da tensão de cisalhamento que age na área da seção transversal da viga e determine a força de cisalhamento resultante que age no segmento AB. O cisalham
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no meio do vão: (a) a maior tensão normal; (b) a maior tensão de cisalhame
Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (a) a maior tensão normal; (b) a tensão de cisalhamento no ponto a ; (c) a maior tensão de cisalhamento.