Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 31
Para a viga composta do Prob. 5.30, determinar a tensão de cisalhamento, no ponto a da aba, do perfil de abas largas mostrado
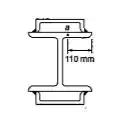
Passo 1
Vamos pegar os dados dos perfis, você pode encontra-lo no final do livro:
Perfil C200X17,1:
Perfil W250X80:
, , mm
Precisamos calcular o momento de inércia, nesse caso temos o momento de inércia do perfil W e do C, porém pro C precisaremos usar o teorema dos eixos paralelos, o centro do perfil C tem a distância do centro da viga composta dada por:
Note que o perfil C está girado e invertido, então o centro está na direção y e deve ser subtraído da largura bf.
Pelo teorema dos eixos paralelos temos:
E com isso a inércia total será:
Onde é a inércia do perfil W.
Passo 2
Precisamos calcular o momento estático para encontrar a tensão no ponto a, vamos então calcular o momento estático pro perfil C acima da solda:
Como o nosso ponto de interesse é o ponto A, precisamos também calcular o momento estático entre a e o perfil C. Como o perfil é ligado nas duas extremidades não dá pra gente simplesmente pegar apenas o ponto A pra direita e calcular o momento estático, a gente precisa criar um ponto simétrico ao A, e dividir a viga em duas partes.
Do ponto A pra direita na mesa, temos:
E como temos que considerar a área em A’:
Enfim calcularemos o momento estático dessa parte e adicionaremos ao calculado. O centro da mesa, onde o ponto A está é:
Enfim:
Passo 3
Por último vamos aplicar a fórmula da tensão de cisalhamento e encontrar o que a gente precisa.
Como a gente pegou as duas seções A e A’, a espessura t será: