Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 126
Para o perfil cantoneira e o carregamento mostrado no Prob 5.8, pede-se: determinar o pontos onde a tensão de cisalhamento é máxima e seus correspondentes valores de tensão; verificar que os pontos obtidos estão localizados sobrea a linha neutra, corresponde ao carregamento dado.
Passo 1
a) Temos que determinar os ponto de cisalhamento máximo e seus correspondentes valores.
Temos a seguinte cantoneira:
Como estamos utilizando um exercício resolvido, irei reutilizar vários cálculos já feitos, logo, caso você desejar querer saber, da onde veio este cálculo, o exercício 5.8 te explicará muito bem.
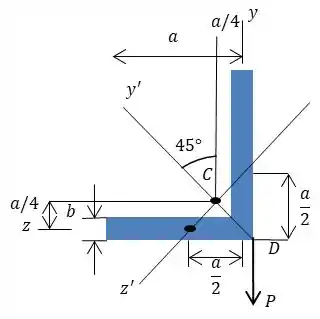
Como a carga é a plicada no ponto , ela causa flexão sem torção na cantoneira.
O que isso quer dizer? Significa que nossas forças de cisalhamento serão apenas oriundas por tensão de cisalhamento por flexão.
Passo 2
a) Temos duas abas para analisar aba vertical, a aba horizontal e a ponta do cotovelo. Estas duas abas possuem tensões de cisalhamento poro flexão por duas componentes e .
Como tensão de cisalhamento combinada na aba vertical está variando com espaço, se diferenciarmos em função de descobriremos o ponto de maior tensão.
Para aba vertical, segundo exercício temos:
Executando a distributiva:
Diferenciando a equação e igualando a zero:
Executando a derivada:
Isolando , para determinar posição do ponto:
Passo 3
Para aba horizontal, aplicando os mesmos passos feitos no passo 2. Mas, aqui iremos diferenciar em função de , pois estamos lidando com a aba horizontal:
Pegando a equação de tensão combinada do exercício 5.8, temos:
Executando a distributiva:
Diferenciando a equação e igualando a zero:
Isolando :
Passo 4
Como temos suas posições, vamos determinar seus respectivos valores.
Para isto iremos simplesmente substituir os valores que encontramos de e nas equações de tensão do exercício.
Para aba vertical:
Substituindo :
Passo 5
Executando os mesmo passos do passo 4, só que para aba horizontal, temos:
Substituindo :
Passo 6
Por último, temos o cotovelo que sua posição representa e .
Aplicando na aba horizontal:
Aplicando na aba vertical:
Passo 7
b) temos que determinar as coordenada e que interceptam a linha neutra.
Temos que localizar nossa linha neutra, para isto, sabemos a linha neutra, passa diretamente no centroide da nossa. A diferença do ângulo com resultara no ângulo necessário para determinar a posição correta de .
Mais ou menos está situação:
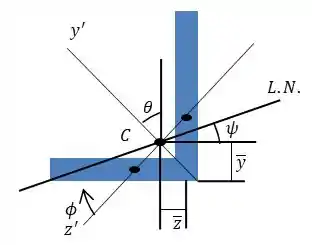
Para determinar , temos a seguinte relação:
Como , e :
Como e simplificando temos:
Executando o arco tangente de , temos que:
Passo 8
Determinando :
Finalmente poderemos determinar as coordenadas que interceptam a linha neutra, para linha vertical:
Para coordenada horizontal:
Resposta
a)Pontos onde o cisalhamento é máximo:
Valor do cisalhamento:
b)Posição da coordenadas que interceptam a linha neutra: