Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 58
O perfil em U é submetido a um cisalhamento . Determine o fluxo de cisalhamento desenvolvido no ponto A
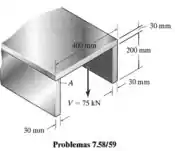
Passo 1
Dados da questão: .
A questão pede o fluxo de cisalhamento no ponto A:
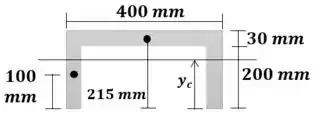
Estratégia de resolução: Vamos começar calculando as propriedades geométricas da seção: Centroide, Momento de Inércia. Depois podemos calcular Momento Estático no ponto de interesse. Por fim, usamos a equação de fluxo de cisalhamento para encontrar o
Passo 2
Primeiro, calculamos o centroide.
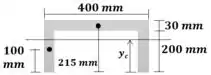
Passo 3
Agora calculamos o momento de inércia em relação ao centroide
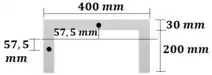
Passo 4
A figura abaixo ilustra o comportamento do fluxo de cisalhamento.
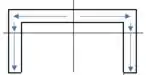
A seção de interesse está destacada abaixo. Vamos pegar apenas um dos lados, pois uma vez que as setas de fluxo de cisalhamento têm direções opostas, se pegarmos os dois lados elas não representarão o fluxo no ponto .
Passo 5
Agora basta aplicar a equação de fluxo de cisalhamento