Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 57
Uma força de cisalhamento é aplicada à viga-caixão simétrica. Determine o fluxo de cisalhamento em C.
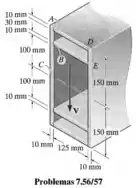
Passo 1
Dados da questão:
A questão pede o fluxo de cisalhamento em C
Estratégia de resolução:
- Vamos calcular o momento de inércia da seção transversal
- Calcular o momento estático em C
- Calcular o fluxo de cisalhamento em C
Passo 2
Como a figura é simétrica, não é preciso calcular o centroide.
O momento de inércia é:
Passo 3
Agora vamos calcular os centroides de cada seção. Observe que somente metade da área deve ser selecionada, já que a outra metade tem fluxo de cisalhamento em sentido inverso.
Seção A:
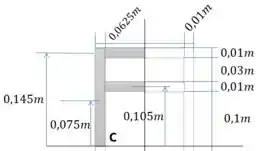
Passo 4
Finalizamos a questão aplicando a equação de fluxo de cisalhamento:
Resposta
Exercícios de Livros Relacionados
Os mancais em A e B exercem somente as componentes x e z das forças sobre o eixo de aço. Determine, com aproximação de 1m m , o diâmetro do eixo, de modo que ele possa resistir às cargas das engrenage
A viga em balanço tem seção transversal circular. Se ela suportar uma força P em sua extremidade, determine seu raio y em função de x, de modo que seja submetida a uma tensão de flexão máxima constant
Trace os diagramas de força cortante e momento fletor para o eixo, em seguida, determine o diâmetro exigido com aproximação de 1m m se σ a d m = 140M P a e τ a d m = 80M P a . Os mancais em A e B exer
A viga simplesmente apoiada é feita de madeira com tensão de flexão admissível σ a d m = 8M P a e tensão de cisalhamento admissível τ a d m = 750k P a . Determine suas dimensões se ela tiver de ser re
Selecione no Apêndice B a viga com avanço de abas largas de aço que tenha o menor peso e que suportará com segurança as cargas. Considere que o apoio em A é um pino e que o apoio em B é um rolete. A t