Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 47

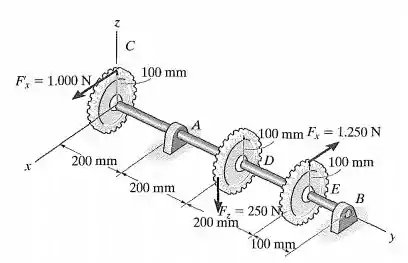
O eixo é suportado por mancais em A e B que exercem sobre o eixo somente as componentes da força nas direções x e z . Se a tensão normal admissível para o eixo for σ a d m = 105   M P a , determine, com aproximação de 1   m m , o menor diâmetro do eixo que suportará a carga da engrenagem. Use a teoria de falha da tensão de cisalhamento máxima com τ a d m = 42   M P a .

Passo 1

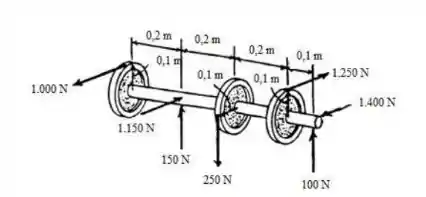
Fala aí galera, vamos para mais uma resolução para você ficar craque nessa matéria. Este problema é simples e pequeno, só temos que ter atenção. Primeiramente, precisamos fazer o nosso querido DCL (Diagrama de corpo livre):

Passo 2

O próximo passo é calcular as reações nos apoios A . Para isso, vamos usar a equação de momento, dada por:

∑ M B = 0 - 1250 i × 0,1 j + - 250 k × 0,3 i + A z k - A x i 0,5 j + ( 1000 i × 0,7 j ) = 0 75 - 0,5 A z i + 575 - 0,5 A x k = 0

Com isso, temos que:

575 - 0,5 A x = 0 A x = 150   k N

75 - 0,5 A z = 0 A Z = 1150   k N

Deixando claro que o nosso foco aqui não é treinar contas, mas a teoria. Logo, as operações foram simplificadas.

Passo 3

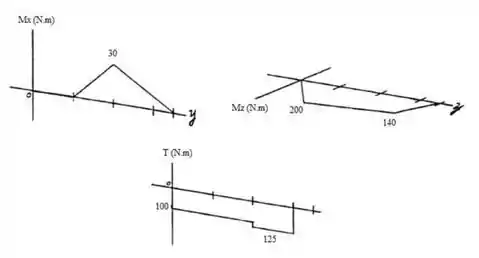
Com as reações dos apoios calculadas, vamos esboçar os diagramas de momento fletor para M x , M z e T :

M x = 0   N . m

M z = 200   N . m T = 100   N . m

Passo 4

Por fim, vamos calcular o momento resultante, dado por:

M = M y 2 + M z 2 M = 0 2 + 200 2 M = 200   N . m

Agora, precisamos encontrar o raio do eixo, para depois calcularmos o diâmetro. Sabendo que o raio do eixo é dado por:

c = 2 π τ a d m M 2 + T 2 1 3 c = 2 π × 42 × 10 6 200 2 + 100 2

c = 15,02   m m  

d = 2 c d = 2 × 15,02 d ≅ 31   m m    

Resposta

d ≅ 31   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma viga extrudada de seção transversal mostrada, determinar:A localização do centro de cisalhamento O A distribuição das tensões de cisalhamento, causadas por uma força vertical V de 2,5k N apli
Para uma viga extrudada, com a seção transversal mostrada, determinar:A distribuição de tensões de cisalhamento, causando pela força cortante vertical V, aplicada em O.
Para uma viga extrudada, com a seção transversal mostrada, determinar:A localização do centro de cisalhamento O.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A tensão de cisalhamento no ponto A