Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 49

A polia acoplada à extremidade do eixo está sujeita à carga mostrada na figura. Se os mancais em A e B exercerem somente as componentes y e z da força sobre o eixo, determine o torque de equilíbrio T na engrenagem C e então determine, com aproximação de 1   m m , o menor diâmetro do eixo que suportará a carga. Use a teoria de falha de energia de distorção máxima com σmáx = 80 MPa.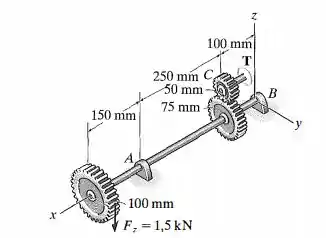

Passo 1

Fala aí galera, vamos para mais uma resolução para você ficar craque nessa matéria. Este problema é simples e pequeno, só temos que ter atenção. Primeiramente, precisamos fazer o nosso querido DCL (Diagrama de corpo livre):

Passo 2

O próximo passo é calcular o torque de equilíbrio:

50 F = T F = T 50

T ' = 75 F = 75 × T 50 = 1,5 T

∑ M = 0 T ' - 150 = 0 1,5 T - 150 = 0 T = 100   N

Passo 3

Com as reações dos apoios calculadas, vamos esboçar os diagramas de momento fletor para M x , M z e T :

M y = 225   N . m

M z = 0   N . m T = 150   N . m

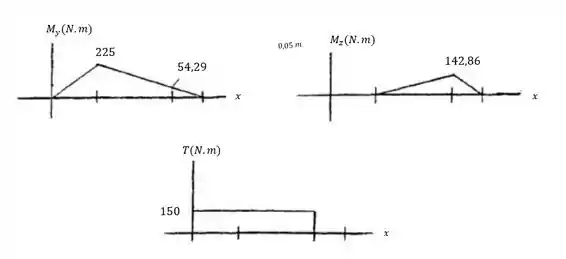
Passo 4

Por fim, vamos calcular o momento resultante, dado por:

M = M y 2 + M z 2 M = 225 2 + 0 2 M = 225   N . m

Agora, precisamos encontrar o raio do eixo, para depois calcularmos o diâmetro. Sabendo que o raio do eixo é dado por:

c = 4 π 2 ( σ a d m ) ²     4 M 2 + 3 T 2 1 6 c = 4 π 2 80 × 10 6 2   4 × 2 25 2 + 3 × 1 5 0 2   1 6 c = 16,05   m m

d = 2 c d = 2 × 1 6,05 d ≅ 31   m m    

Resposta

d ≅ 31   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga extrudada tem seção transversal como mostrado e uma espessura de parede constante e igual a 3 m m . Para uma força cortante vertical de 10 k N , determinar:A máxima tensão de cisalhamento na
Uma viga com a seção transversal mostrada é submetida a uma força cortante vertical V . Determine (a) a linha horizontal ao longo da qual a tensão de cisalhamento máxima. (b) a constante k na expressã
A viga fabricada mostrada é feita colando duas tiras de madeira compensada de 20 x 250 mm e duas pranchas de 50 x 100 mm. Sabendo que a tensão de cisalhamento média nas juntas coladas é de 350 kPa, de
Uma placa de 2 mm de espessura é dobrada conforme mostrado, e então usada como viga. Para uma força cortante vertical de 5 kN, determine a tensão de cisalhamento nos cinco pontos indicados e esquemati
Uma viga de alumínio extrudada tem a seção transversal mostrada na figura. Sabendo que a força cortante vertical na viga é 150 kN, determine a tensão de cisalhamento no (a) ponto a e (b) ponto b.