Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 59

Para a viga mostrada na figura, determine (a) a intensidade P das duas forças direcionadas para cima para que o valor absoluto máximo do momento fletor na viga é o menor possível, (b) o valor correspondente de | M | max.

Figura P7.59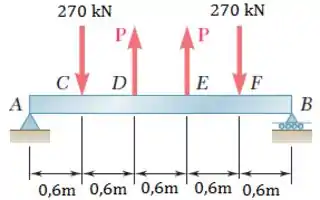

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Novamente é interessante notar a simetria do carregamento em relação a um eixo vertical que passa pelo centro da viga Isso facilita a analise e construção do diagrama de dmomento fletor.

Passo 2

Monte o diagrama de corpo livre da viga:

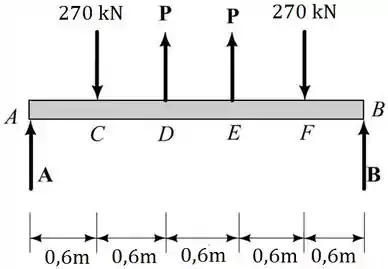
Passo 3

Devido a simetria da viga e carregamento:

A = B = 270 - P k N

Analisando a região AC, o momento fletor máximo ocorre no ponto C:

+ ↺ ∑ M c = 0

M C - ( 270 - P ) ( 0,6 ) = 0

M C - 162 + 0,6 P = 0

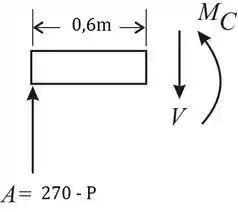
M C = 162 - 0,6 P .....................................(Eq. 1)

O maior momento fletor negativo ocorre no eixo de simetria da viga.

+ ↺ ∑ M E = 0

M E - 270 - P 1,5 + 270 0,9 - P ( 0,3 ) = 0

M E - 405 + 1,5 P + 243 - 0,3 P = 0

M E = 162 - 1,2 P .....................................(Eq. 2)

Passo 4

Iguale M C   e - M E e resolva.

162 - 0,6 P = - ( 162 - 1,2 P )

1,8 P = 324

P = 180   k N

Passo 5

O valor de P pode ser substituído na Eq. 1 para obter | M | max.

M C = 162 - 0,6 P

M C = 162 - 0,6 ( 180 )

M C = 54   k N . m

Passo 6

Agora podemos elaborar o diagrama de momento fletor:

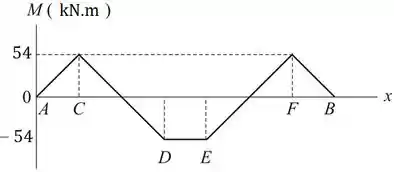
Resposta

  1. O valor máximo de P é:

    2. P = 180   k N

  2. O valor de | M | max é:

| M | m a x = 54   k N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cabo de 30m é pendurado entre dois edifícios como mostra a figura. A tensão máxima encontrada é 500N e o ponto mais baixo do cabo observado está a 4m acima do solo. Determine (a) a distância horizo
Mostre que a curva assumida por um cabo que carrega uma carga distribuída w ( x ) é definida por pela equação diferencial d 2 y / d x 2 = w ( x ) / T 0 , sendo T 0 a tração no ponto mais baixo.
Se o peso por unidade de comprimento do cabo A B é w 0 / cos 2 ⁡ θ , prove que a curva formada pelo cabo é um arco de círculo. (Dica: use a propriedade indicada no Problema 7.124 ).
Um cabo, que tem peso por unidade de comprimento igual a 30N / m , é suspenso entre dois pontos de igual elevação, distanciados 48m entre si. Determine a menor flecha possivel do cabo se a tração máxi
Um motor M é usado para lentamente o cabo mostrado na figura. Sabendo que a massa por unidade de comprometimento do cabo é 0,4k g / m , determine a tração máxima no cabo quando h = 5m .