Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 83
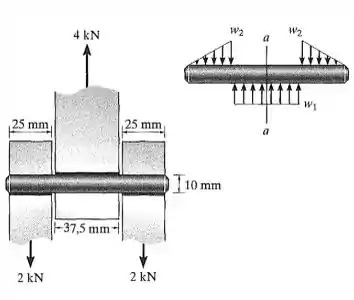
O pino é usado para interligar os três elos. Devido ao desgaste, a carga é distribuída na parte superior e inferior do pino, como mostra o diagrama de corpo livre. Se o diâmetro do pino for 10 mm, determine a tensão de flexão máxima na área da seção transversal na seção central a-a. Para resolver o problema, em primeiro lugar, é necessário determinar as intensidades das cargas w1 e w2.
Passo 1
Para determinar w1 e w2, utilizaremos as equações de equilíbrio:
Passo 2
Vamos então determinar o momento na seção:
Passo 3
Agora, podemos determinar a tensão:
Resposta
Exercícios de Livros Relacionados
Determinar momento plástico M p , da viga da Prob 4.8, considerando que o aço seja elastoplásticos, com uma tensão de escoamento de 250M P a .
Determinar o momento plástico M p , para uma viga do Prob 4.16, considerando que a viga é feita de um aço que é elastoplásticos, com uma tensão de escoamento de 270M P a
Determinar o momento plástico Mp, de uma viga de aço de seção transversal mostrada,quando a viga é encurvada em torno do eixo horizontal. Assumir que o aço é elastoplástico, com uma tensão de escoamen
Considerando a viga do problema 77, é aplicado um momento igual ao momento plástico Mp da viga e, depois removido. Usando uma tensão de escoamento de 290 MPa, determinar a tensão residual para y1 = 25
Para a viga do problema 79, um momento igual ao momento plástico Mp da viga é aplicado e, depois, removido. Usando uma tensão de escoamento de 300MPa, determinar a tensão residual para y1 = 24mm e y2