Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 18

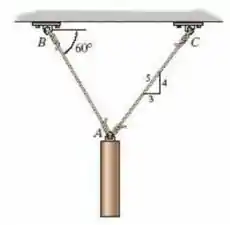
Os cabos de aço A B e A C sustentam a massa de 200   k g . Se a tensão axial admissível para os cabos for σ a d m = 130     M P a , determine o diâmetro exigido para cada cabo. Além disso, qual é o novo comprimento do cabo A B após a aplicação da carga? Considere que o comprimento não alongado de A B seja 750   m m . E a ç o = 200   G P a .

Passo 1

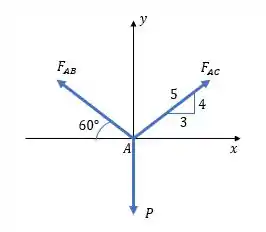
Fala aí pessoal, bora para mais um exercício de resmat. Primeiro, vamos esboçar o DCL no ponto A , temos:

Passo 2

Agora, vamos aplicar as equações de equilíbrio para determinar os valores das forças nos cabos. Para o eixo x , temos:

∑ F x = 0

- T A B cos ⁡ 60 ° + 3 5 T A C = 0

Já para o eixo y , temos:

∑ F y = 0

T A B sen ⁡ 60 ° + 4 5 T A C - P = 0

Como :

P = M A g

P = 200 × 9,81

P = 1962   N

Substituindo, temos:

T A B sen ⁡ 60 ° + 0,8 T A C - 1962 = 0

Com isso, podemos observar que temos um sistema de duas equações e duas incógnitas.

- T A B cos ⁡ 60 ° + 0,6 T A C = 0   ( 1 )

T A B sen ⁡ 60 ° + 0,8 T A C = 1962   ( 2 )

Isolando T A C :

T A C = T A B cos ⁡ 60 0,6 = 0,833 T A B

Substituindo na eq. 2:

T A B s e n 60 + 0,8 × 0,833 T A B = 1962

E então:

T A B = 1962 1,532 = 1280,17 N

Agora encontrando T A C :

T A C = 0,833 T A B = 0,833 × 1280,17 = 1066,38   N

Passo 3

Em seguida, podemos calcular a tensão admissional em A B , dada por a fim de encontrarmos o diâmetro do cabo A B . Fica assim:

σ a d m = T A B A A B

Onde:

A A B = π d A B 2 4 d A B = 4 T A B π ∙ σ a d m

d A B = 4 1280,177   N π ∙ 130

E então:

d A B = 3,54   m m

Para encontrarmos o diâmetro para o cabo A C , basta repetirmos o processo:

d A C = 4 T A C π ∙ σ a d m

d A C = 4 1066,77   N π ∙ 130

d A C = 3,23   m m

Passo 4

Para encontrarmos o novo comprimento do cabo A B , vamos utilizar a Lei de Hooke, temos:

ε = σ E

ε = 130 × 10 6 200 × 10 9

ε = 0,00065   m m / m m

Logo, o novo comprimento vai ser:

L A B ' = 1 + ε L A B

L A B ' = 1 + 0,00065 [ m m m m ] 750   m m

L A B ' = 750,49   m m

Resposta

L A B ' = 750,49   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de alumínio não deve sofrer um estiramento maior que 0,05 in quando submetido a tensão de tração. Sabendo que E = 10,1x10 6 psi e que a tensão normal máxima admissível é de 14 ksi, determine (
Um bloco de 10 in. de comprimento e seção transversal de 1,8x1,6i n deve suportar uma força de compressão centrada P. O material a ser utilizado é um bronze para o qual E = 14x10 6 p s i . Determine a
Duas marcas de referência são colocadas a exatamente 250 mm uma da outra, em uma barra de alumínio haste com E=73G P a e resistência última de 140 MPa com diâmetro de 12 mm. Sabendo que a distancia en
O sólido mostrado foi cortado de uma chapa de vinil com 1 4 in de espessura (E = 0,45x10 6 p s i ) e é submetido a uma tração de 350 lb. Determine (a) a deformação total do sólido, (b) a deformação de
Um cabo de aço de 4,8 ft de comprimento de ¼ in de diâmetro é submetido a uma ação de tração de 750 lb. Sabendo que E=29X10 6 p s i . Determine (a) o alongamento do arame, (b) a correspondente tensão