Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 54b
Uma placa anelar de latão de espessura é usada para conectar o eixo de latão , de comprimento e raio , ao tubo de latão de comprimento , raio interno e espessura Sabendo-se que um torque é aplicado à extremidade do eixo AB, e que a extremidade D do tubo CD é engastada, determinar: (a) a máxima tensão de cisalhamento no sistema placa-tubo; (b) o ângulo de rotação da extremidade A.
Passo 1
O item B é uma pegadinha.
Apesar da questão pedir a rotação da extremidade A, o que ela realmente quer é a rotação absoluto entre A e D.
Ou seja, vamos precisar calcular as rotações de todas as seções do sistema.
Passo 2
Primeiro vamos calcular o ângulo de torção da barra AB
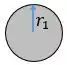
Já temos o momento polar de inércia:
E calculamos o ângulo de torção
Passo 3
Para calcular a deformação na placa, vamos usar a equação que deduzimos na questão anterior (Problema 3.53b)
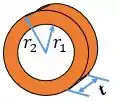
Passo 4
No tubo CD
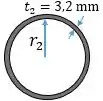
Já temos o momento de inércia polar:
Basta calcular o ângulo:
Passo 5
O ângulo de torção total será: