Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 51
As extremidades A e D de dois eixos maciços de aço, AB e CD, estão engastadas enquanto as extremidades B e C são conectadas por engrenagens, como indicado. Sabendo-se que um torque T de 4 kNm é aplicado na engrenagem B, determinar a máxima tensão de cisalhamento: (a) no eixo AB; (b) no eixo CD.
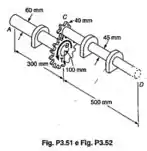
Passo 1
Como quase todas as questões de torção, vamos começar calculando os momentos de inércia dos eixos.
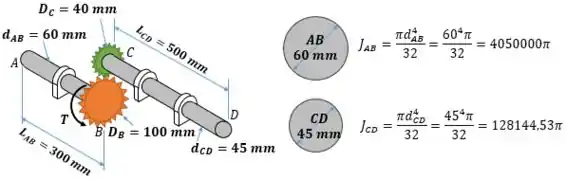
Passo 2
Agora vamos pensar um ponto na física do problema.
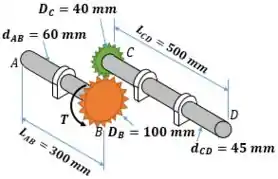
Um torque é aplicado diretamente no ponto B. Mas ao contrário do que parece, nem todo o valor de é transmitido para o eixo AB. Somente parte desse torque é transmitido para o eixo AB e outra parte é transmitida para o eixo CB. Como descobrir o quanto de torque foi para cada eixo?
A primeira coisa a se notar é que as duas extremidades e são engastadas. Logo esse é um sistema estático! Então vamos nos aproveitar das CONDIÇÕES ESTÁTICAS.
Agora vamos desenhar um diagrama de corpo livre de cada uma das engrenagens:
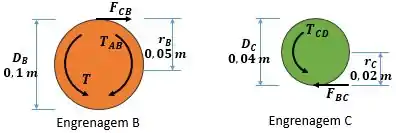
Na engrenagem a questão nos diz que um torque é aplicado nessa engrenagem. Essa é uma estrutura estática, então, como reação surgirá um torque que vamos chamar de chamar esse torque de E devido ao contato entre as duas engrenagens surge uma força .
A engrenagem sofre a força de contato vinda da engrenagem B, como reação surge um torque na engrenagem C:
A gente já sabe que então se aplicarmos o somatório de momentos em cada uma das engrenagens teremos:
Mas nesse sistema temos três incógnitas e e apenas duas equações. Ainda não dá para resolver.
Passo 3
Para resolver esse sistema vamos precisar de mais uma equação. Quando estamos trabalhando com engrenagens devemos considerar as CONDIÇÕES CINEMÁTICAS.
Esta condição diz que o ângulo de torção de duas engrenagens acopladas é proporcional da seguinte forma:
A deformação das engrenagens é desprezível, então as deformações e são as deformações das barras AB e CD.
Então, vamos aplicar a equação do ângulo de torção:
Simplificamos o G dos dois lados, e isolamos o
Passo 4
Show!
Agora temos um sistema completo:
E resolvendo o sistema chegamos nos resultados:
Passo 5
E agora é só utilizar a equação da tensão de cisalhamento para calcular as tensões:
No eixo AB:
No eixo CD: