Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 18
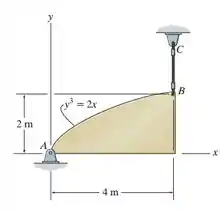
A placa é feita de aço com uma densidade de kg/m³. Se a espessura da placa é mm, determine as componentes horizontal e vertical da reação no pino e a tração no cabo .
Passo 1
Vamos tomar nosso elemento diferencial como a área em cinza mostrada na figura:
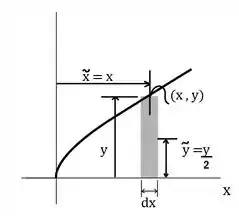
Essa área é dada por:
Sabendo que , nosso fica:
O centroide do nosso elemento diferencial fica em:
Aqui, vamos usar o pino como orientação, não importa a altura do centroide, apenas sua distância em , já que usaremos momento, por isso não precisamos do .
Passo 2
Vamos encontrar nossa área:
Logo, a massa da placa pode ser obtida por:
Onde é a densidade e a espessura dada no enunciado:
Passo 3
E agora encontramos nosso centroide :
Como a placa é uniforme, o centro de gravidade coincide com o centroide.
Passo 4
Vamos agora encontrar a reação no pino e a tração no cabo, usando as equações de equilíbrio, sabemos que:
Adotando o sentido anti-horário positivo, temos aqui o cabo agindo no sentido anti-horário a uma distância de m do pino e o peso da placa no sentido horário com a distância encontrada do centroide:
Como não temos forças agindo em :
E por último, usamos o somatório de forças em para encontrar a reação no pino, que aqui temos a tração do cabo e o peso: