Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 71
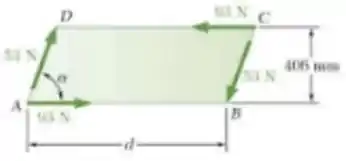
Uma placa em forma de paralelogramo sofre a ação de dois binários. Determine o momento do binário formado pelas duas forças de 93 N, a distância perpendicular entre as forças de 53 N fazendo com que o momento resultante seja zero, e o valor de para quando d = 1,06 m e M = 8,1 N.m.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora!
Nessa questão temos dois binários atuando em nossa placa. Um deles é dado pelas forças de e o outro binário é dado pelas forças de .
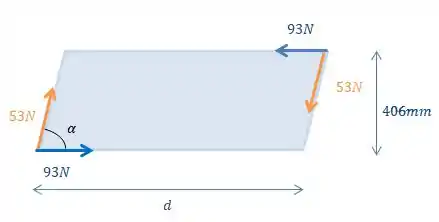
E para calcular os nossos momentos gerados por esses binários vamos usar a fórmula:
Sendo a força do binário e a distância perpendicular entre as forças do binário.
Passo 2
Ok, a primeira parte da questão, nos pede para calcular o momento do binário formado pelas duas forças de . Vou chamar esse momento de para ficar mais fácil, beleza?
Onde é a nossa força de e é a distância perpendicular entre as forças do binário, que é dada no desenho, é o próprio , que convertendo para metros fica...
E como esse momento ocorre no sentido anti-horário, vou considera-lo aqui como sendo positivo mesmo!
Passo 3
Agora a questão nos pediu a distância perpendicular entre as forças de de forma que o momento resultante seja zero, ou seja, queremos que:
E como os momentos gerados por esses binários possuem direção opostas, isso vai acontecer se:
Onde é o momento do meu binário de forças formado pelas forças de .
Podemos escrever como sendo:
Agora é preciso tomar cuidado aqui hein!! Essa distância é a distância perpendicular entre as forças de e que como essas forças estão inclinadas, essa não é a distância do nosso desenho!
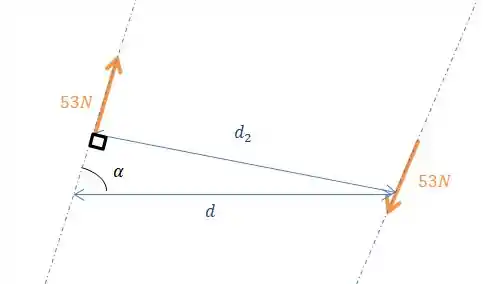
Mas felizmente, é a distância perpendicular que queremos encontrar nessa parte do exercício, então, vamos encontrar esse !
Passo 4
Pronto!! Agora vamos fechar essa questão, nessa última parte ele pediu que a gente encontre o valor desse ângulo para o caso em que e que .
Bom, vamos por partes...
Sabemos que o momento resultante vai ser a soma dos momentos e que o momento do binário de é no sentido anti-horário (positivo) e do binário de é no sentido horário (negativo).
Sendo assim, é preciso que o valor em módulo do momento desse binário seja de
Agora, vamos calcular esse momento:
Mas se liga, aqui não vamos trabalhar com a distância perpendicular e sim com a distância dada no desenho, se a gente olhar para o desenho, podemos relacionar essas distâncias, pois temos ali um triângulo:
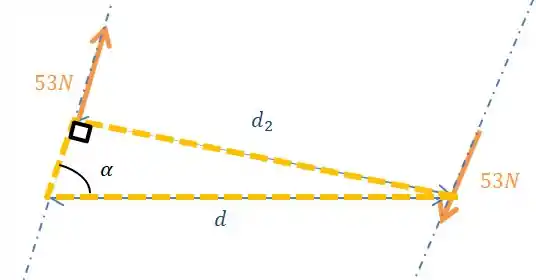
Da onde temos a relação:
Agora é só substituir na nossa expressão, pois temos o valor de
E portanto o nosso ângulo vai ser:
E prontinho, fechamos mais uma!