Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 184

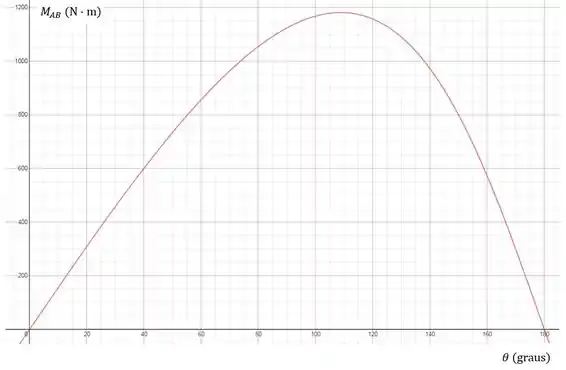
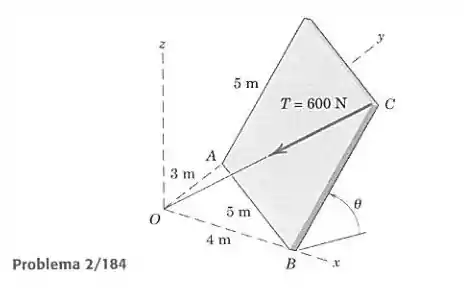
A placa retangular está inclinada em relação a sua borda inferior por um cabo sob tração constante de 600 N. Determine e faça um gráfico do momento desta força trativa em relação à borda inferior A B da placa, para a faixa 0 ° ≤ θ ≤ 180 °

Passo 1

Devemos obter o momento em torno de B causado pela tração aplicada na linha O C . Como a linha de ação de força passa pela origem, podemos calcular o momento da seguinte maneira:

M → B = T → × r → B O = - T → × r → B

Então devemos obter a expressão do vetor T → , em seguida o vetor r → B , e após obtido o momento M → B , o projetaremos na reta A B .

Passo 2

Primeiro vamos encontrar a expressão da tração T → . Como ela está na direção C O , podemos escrevê-la assim:

T → = T n → C O

Sendo n → C O o vetor unitário que tem a direção C O . Calculamos esse vetor assim:

n → C O = r → C O r C O

Onde r C O é o módulo do vetor r → C O . Precisamos das coordenadas do ponto C . A coordenada z de C é igual a 5 sen ⁡ θ . Se olharmos “de cima” o desenho, temos essa configuração:

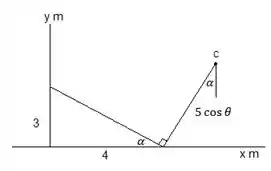
Então:

r → C O = - r → C = - 4 + 5 cos ⁡ θ sen ⁡ α i ^ - 5 cos ⁡ θ cos ⁡ α j ^ - 5 sen ⁡ θ k ^

⇒ r → C O = - 4 + 3 cos ⁡ θ i ^ - 4 cos ⁡ θ j ^ - 5 sen ⁡ θ k ^

Passo 3

Agora calculamos o módulo:

r C O = 4 + 3 cos ⁡ θ 2 + 4 cos ⁡ θ 2 + 5 sen ⁡ θ 2

= 16 + 24 cos ⁡ θ + 9 cos 2 ⁡ θ + 16 cos 2 ⁡ θ + 25 sen 2 ⁡ θ

= 16 + 24 cos ⁡ θ + 25 sen 2 ⁡ θ + cos 2 ⁡ θ = 41 + 24 cos ⁡ θ

Já podemos calcular então o vetor T → :

T → = T n → C O = T r → C O r c o = 600 41 + 24 cos ⁡ θ ( - 4 + 3 cos ⁡ θ i ^ - 4 cos ⁡ θ j ^ - 5 sen ⁡ θ k ^ )  

Passo 4

Calculamos o momento como foi explicado no passo 1:

M → B = T → × r → B O = - T → × r → B

⇒ M → B = - 600 41 + 24 cos ⁡ θ 4 i ^ × - 4 + 3 cos ⁡ θ i ^ - 4 cos ⁡ θ j ^ - 5 sen ⁡ θ k ^

= - 600 41 + 24 cos ⁡ θ i ^ j ^ k ^ 4 0 0 - 4 - 3 cos ⁡ θ - 4 cos ⁡ θ - 5 sen ⁡ θ

= - 600 41 + 24 cos ⁡ θ - 16 cos ⁡ θ k ^ + 20 sen ⁡ θ j ^ = 2400 41 + 24 cos ⁡ θ - 5 sen ⁡ θ j ^ + 4 cos ⁡ θ k ^

Passo 5

Já encontramos então o momento em torno de B . Basta encontrarmos a projeção em A B . Para projetarmos, fazemos o produto interno do vetor pelo unitário na direção A B :

M A B = M → B ⋅ n → A B

Temos:

n → A B = r → A B r A B = 4 i ^ - 3 j ^ 5

Então, finalmente:

M A B = M → B ⋅ n → A B = 2400 41 + 24 cos ⁡ θ - 5 sen ⁡ θ j ^ + 4 cos ⁡ θ k ^ ⋅ 4 i ^ - 3 j ^ 5

⇒ M A B = 480 41 + 24 cos ⁡ θ - 5 sen ⁡ θ j ^ + 4 cos ⁡ θ k ^ ⋅ 4 i ^ - 3 j ^

⇒ M A B = 480 41 + 24 cos ⁡ θ 15 sen ⁡ θ ⇒ M A B = 7200 sen ⁡ θ 41 + 24 cos ⁡ θ

Resposta

M A B = 7200 sen ⁡ θ 41 + 24 cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com a peça cilíndrica P , que pesa 1500 N, em sua garra, o braço robótico gira em torno de O na faixa - 45 ° ≤ θ ≤ 45 ° com o ângulo em A fixo em 120°. Determine, e mostre em um gráfico (em função de
Um mastro de uma bandeira com uma estrutura triangular leve está mostrado aqui em uma posição arbitrária durante sua elevação. A força trativa de 75 N no cabo de elevação se mantém constante. Determin
A força trativa T no cabo A B é mantida em um valor constante de 120 N. Determine o momento M O dessa força trativa em torno do ponto O na faixa 0 ° ≤ θ ≤ 90 ° . Faça um gráfico das componentes x , y
A força F está direcionada de A para D e D pode se movimentar de B até C , sendo sua posição medida pela variável s . Considere a projeção de F sobre a linha E F como função de s . Em particular, dete