Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 189
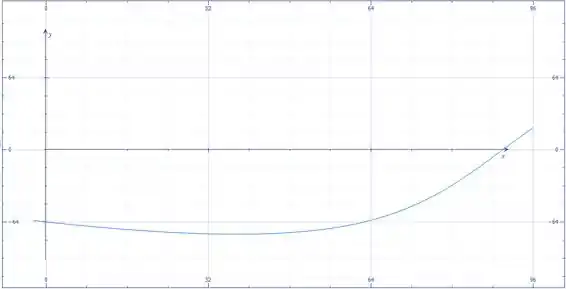
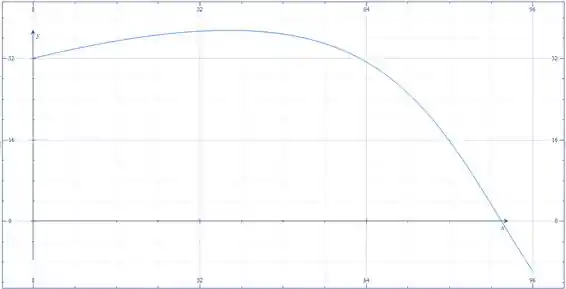
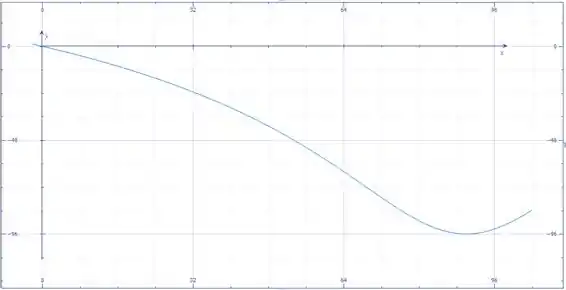
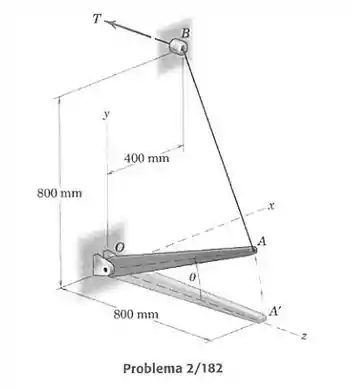
A força trativa no cabo é mantida em um valor constante de 120 N. Determine o momento dessa força trativa em torno do ponto na faixa . Faça um gráfico das componentes , , e de em função de .
Passo 1
Para obtermos a expressão vetorial da tração e assim conseguirmos calcular o momento em relação a , precisamos primeiro definir a posição do ponto em função do ângulo . O ponto percorre um círculo de raio igual a 0,8 m em volta do ponto , no plano sendo o ângulo entre e . Então as coordenadas de são:
Passo 2
Agora que sabemos a posição de , podemos obter o vetor unitário que tem a mesma direção que a força . Vamos então calcular , sendo o módulo do vetor :
Então:
Passo 3
Como nossa força tem um módulo constante igual a 120 N e a direção dada por , então podemos escrevê-la assim:
Podemos então calcular nosso momento , aplicando o produto vetorial :
Passo 4
Agora mostramos os gráficos das componentes e de :
