Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 184

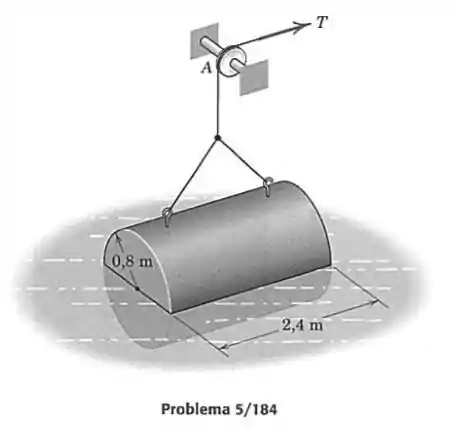
184- O cilindro sólido de concreto com de comprimento e de diâmetro é sustentado em uma posição semi-submersa em água doce por um cabo que passa sobre uma polia fixa em . Calcule a força trativa no cabo. O cilindro é impermeabilizado por um revestimento de plástico. (Consulte a Tabela , Apêndice D, quando necessário.)

Passo 1

Vamos fazer o diagrama de corpo livre no cilindro para entendermos o que está sendo realizado nesse momento.

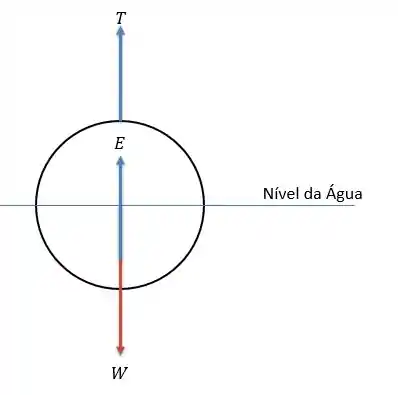
Pela somatória das forças verticais temos:

Onde é a força de tração, a força de empuxo (ou flutuabilidade) e o peso do cilindro.

Passo 2

O peso do cilindro pode ser calculado como:

Porém não temos informações sobre a massa do cilindro, então precisamos substituir sua massa pela relação entre a sua densidade e seu volume:

Logo:

Onde a densidade do cilindro é a densidade do concreto e no anexo conseguimos ver que é de , logo o peso do cilindro será de:

Passo 3

Para calcular o empuxo temos que fazer a seguinte conta:

Onde o do liquido, que é a agua doce, pelo anexo é de e o volume submerso é a metade da do cilindro (pelo desenho).Logo:

Passo 4

Substituindo os valores das forças teremos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

188- Uma esfera sólida e homogênea de raio r está apoiada sobre o fundo de um tanque que contém um líquido de massa específica ρ l , que é maior do que a massa específica ρ s da esfera. A medida que o

187- Uma seção vertical de um tanque para drenagem do óleo está mostrada. A placa de acesso cobre uma abertura retangular, que tem uma dimensão de 400m m normal ao plano do papel. Calcule a força tota

192- Determine a força total R exercida sobre a janela triangular pela água doce no tanque. O nível da água coincide com o topo da janela. Determine, também, a distância H , desde R até o nível da águ

189- A comporta retangular, mostrada em seção, tem 3m de comprimento (perpendicular ao plano do papel) e bascula em relação a sua borda superior B . A comporta divide um canal, que a esquerda leva a u

191- O projeto de uma plataforma flutuante de perfuração de petróleo consiste em dois flutuadores retangulares e em seis colunas cilíndricas, que suportam a plataforma de trabalho. Quando lastreada, a