Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 179

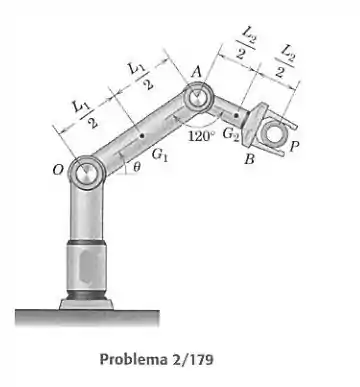
Com a peça cilíndrica P , que pesa 1500 N, em sua garra, o braço robótico gira em torno de O na faixa - 45 ° ≤ θ ≤ 45 ° com o ângulo em A fixo em 120°. Determine, e mostre em um gráfico (em função de θ ), o momento em O devido aos efeitos combinados do peso da peça P , do peso de 600 N do elemento O A (centro de massa em G 1 ) e do peso de 250 N do elemento A B (centro de massa em G 2 ). A garra é incluída como parte do elemento A B . Os comprimentos L 1 e L 2 são 900 mm e 600 mm respectivamente. Qual é o valor máximo de M O e em qual valor de θ ocorre esse máximo?

Passo 1

O que queremos aqui é achar o momento causado por cada um dos três pesos em relação ao ponto O e depois somar tudo. Vamos então calcular um por um.

Passo 2

Primeiro temos o peso de 600 N aplicado em G 1 . A distância horizontal do ponto O at´r o ponto G 1 é:

d 1 = L 1 2 cos ⁡ θ = 0,45 cos ⁡ θ

Então o momento é:

M 1 = 600 0,45 cos ⁡ θ = 270 cos ⁡ θ   N ⋅ m ( s e n t i d o   h o r á r i o )

Passo 3

Agora calculamos o momento causado pelo peso de 250 N em G 2 . O ângulo entre o trecho A B e a horizontal é 60 ° - θ , como mostra a figura.

A distância é:

d 2 = L 1 cos ⁡ θ + L 2 2 cos ⁡ 60 ° - θ = 0,9 cos ⁡ θ + 0,3 cos ⁡ 60 ° - θ

Então o momento é:

M 2 = 250 0,9 cos ⁡ θ + 0,3 cos ⁡ 60 ° - θ

= 225 cos ⁡ θ + 75 cos ⁡ 60 ° - θ N ⋅ m ( s e n t i d o   h o r á r i o )

Passo 4

Agora achamos o momento causado pelo peso do cilindro igual a 1500 N.

d 3 = L 1 cos ⁡ θ + L 2 cos ⁡ 60 ° - θ = 0,9 cos ⁡ θ + 0,6 cos ⁡ 60 ° - θ

E finalmente achamos o último momento

M 3 = 1500 0,9 cos ⁡ θ + 0,6 cos ⁡ 60 ° - θ

= 1350 cos ⁡ θ + 900 cos ⁡ 60 ° - θ   N ⋅ m ( s e n t i d o   h o r á r i o )

Passo 5

Agora somamos tudo para achar o momento resultante em O :

M = 270 cos ⁡ θ + 225 cos ⁡ θ + 75 cos ⁡ 60 ° - θ + 1350 cos ⁡ θ + 900 cos ⁡ 60 ° - θ

⇒ M = 1845 cos ⁡ θ + 975 cos ⁡ ( 60 ° - θ )

O gráfico a seguir mostra M em função de θ (em graus):

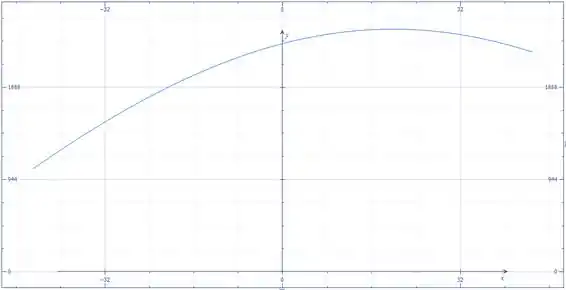
Fazendo uma análise gráfica vemos que M M á x = M 19,9 ° = 2480,6   N ⋅ m

Resposta

M = 1845 cos ⁡ θ + 975 cos ⁡ ( 60 ° - θ )

M M á x = M 19,9 ° = 2480,6   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as coordenadas do ponto no plano x z pelo qual passa a linha de ação da resultante do sistema de forças, para o sistema de forças do Prob. 2/149.
A resultante das duas forças e do torque pode ser representada por um torçor. Determine a expressão vetorial para o momento M do torçor e encontre as coordenadas do ponto P no plano x z pelo qual pass
Na posição mostrada, o virabrequim de um pequeno compressor de dois cilindros está submetido a forças de 400 N e 800 N, exercidas pelas bielas, e um torque de 200 N.m. Substitua esse sistema de carreg
A alavanca de controle O A gira na faixa 0 ° ≤ θ ≤ 90 ° . Uma mola de torção interna exerce um momento de retorno na alavanca em torno do ponto O dado por M = K ( θ + π / 4 ) onde K = 500N ⋅ m m / r a
Um motor, preso ao eixo O faz o braço O A girar na faixa 0 ° ≤ θ ≤ 180 ° ao braço. O comprimento original da mola é de 0,65 m e ela pode suportar tato tração quanto compressão. Se o momento resultante