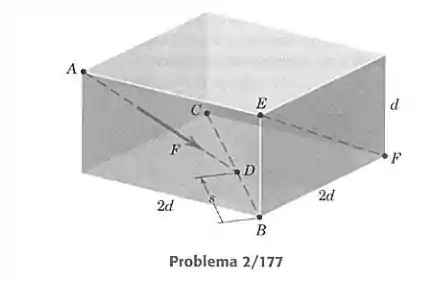
A força F está direcionada de para e pode se movimentar de até , sendo sua posição medida pela variável . Considere a projeção de F sobre a linha como função de . Em particular, determine e mostre em um gráfico em função de , a fração do módulo de que está projetada. Observe que varia de até .

Primeiro devemos achar o vetor . Vamos colocar os eixos coordenados dessa maneira:

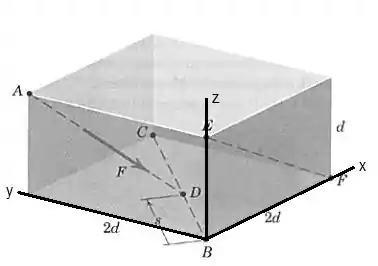
O vetor n será dado pela fórmula:

Sendo o vetor que aponta de para e seu módulo. Podemos considerar o segmento de reta como a reta com indo de a . Nesse caso temos então o que nos leva às coordenadas do ponto em função de :

Então:

O módulo de será então:

Agora conseguimos achar :

Vamos agora encontrar . Novamente vamos fazer:

Agora calculamos o módulo:

E finalmente:

Agora conseguimos calcular . No primeiro passo vimos que:

Então:

Como queremos o resultado em função de , dividimos por em cima e em baixo: