Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 24

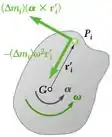
Para uma placa rígida em rotação em torno do centro de massa, mostre que o sistema de forças efetivas consiste de vetores - Δ m i ω 2 r i ' e Δ m i α × r i ' ligados às várias partículas Pi da placa, onde ω e α são a velocidade angular e a aceleração angular da placa, e onde r i ' representa a posição da partícula Pi em relação ao seu centro de massa G. Mostre também, calculando sua soma e a soma de seus momentos em relação a G, que as forças efetivas se reduzem a um binário I - α .

Passo 1

Fala ai pessoal tudo belezinha? O enunciado pede para que a gente mostre também, calculando sua soma e a soma de seus momentos em relação a G, que as forças efetivas se reduzem a um binário I - α .

Para rotação centroide:

a i = a i i + a i n = α × r i ' - ω 2 r i '

Passo 2

As forças eficazes são:

Δ m i a i = Δ m i α × r i - ∆ m i ω 2 r i ' Δ m i α × r i

Σ Δ m i a i = Σ Δ m i α × r i ' - Σ Δ m i ω 2 r i '

= α × Σ Δ m i r i ' - ω 2 Σ Δ m i r i '

Passo 3

Uma vez que G é o centro mestre,

Σ Δ m i r i ' = 0

as forças efetivas se reduzem a um par, momentos sobre G

Σ r i ' × ∆ m i a i = Σ r i ' × ∆ m i α × r i ' - Σ r i ' × ∆ m i ω 2 r i '

r i ' × ∆ m i ω 2 r i ' = ω 2 Δ m i r i ' × r i ' = 0

r i ' × ∆ m i α × r i ' = ∆ m i r i ' 2 α

Passo 4

Portanto,

Σ r i ' × ∆ m i a i = Σ Δ m i r i 2 α = Σ Δ m i r i ' 2 α

Desde

Σ Δ m r i ' 2 = I - ,

o momento do casal é I - α

Resposta

Σ Δ m r i ' 2 = I - ,

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de um disco de 5 pol. de raio é encaixado em uma fenda que forma um ângulo θ = 30 ∘ com a vertical. O disco está em repouso quando é colocado em contato com uma correia transportadora em movime
Resolva o problema 16. 153, assumindo que a direção do movimento do cinturão transportador é revertido.Problema 16.153 - O eixo de um disco de 5 pol. de raio é encaixado em uma fenda que forma um ângu
Cilindros idênticos de massa m e raio r são empurrados por uma série de braços móveis. Assumindo que o coeficiente de atrito entre todas as superfícies seja u
Um ciclista está andando de bicicleta a uma velocidade de 20 mph em uma estrada horizontal. A distância entre os eixos é de 42 in, e o centro de massa do ciclista e da bicicleta está localizado a 26 i
A haste uniforme AB de peso W é liberada do repouso quando β = 70 °. Assumindo que a força de atrito entre a extremidade A e a superfície é grande o suficiente para evitar o deslizamento, determine im