Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 40

A plataforma de 150 kg pode ser considerada como um disco circular. Dois homens, A e B, de 60 kg e 75 kg de massa, respectivamente, estão parados de pé na plataforma quando ela está em repouso. Se eles começam a caminhar em torno das trajetórias circulares com velocidades de v A / P = 1,5   m / s e v B / P = 2   m / s , medidas em relação à plataforma, determine a velocidade angular da plataforma.

Passo 1

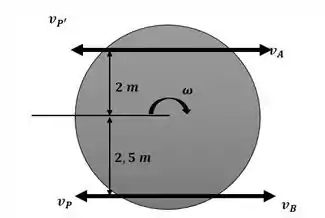
Começaremos o exercício escrevendo as velocidades absolutas dos homens A e B com o auxílio da imagem a seguir:

+ →   v B = v P + v B / P

v B = - ω 2,5 + 2

+ →   v A = v P + v A / P '

v A = ω 2 + 1,5

Passo 2

Agora devemos calcular o momento de inércia do sistema em relação ao ponto O:

I O = 1 2 m r 2 = 1 2 150 3 2

I O = 675   k g . m 2

Passo 3

Uma vez que os impulsos gerado pelos homens são internos ao sistema, podemos aplicar a conservação da quantidade de movimento angular para o sistema:

H 1 O = H 2 O

0 = 75 v B 2,5 - 60 v A 2 - 675 ω

Agora, iremos substituir os valores encontrados para v A e v B no passo 1 nessa última equação para determinar a velocidade angular da plataforma:

75 - ω 2,5 + 2 2,5 - 60 ω 2 + 1,5 2 - 675 ω

ω = 0,141   r a d / s

Resposta

ω = 0,141   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera ricocheteia, como mostrado na figura, após atingir um plano inclinado com uma velocidade vertical v 0 de intensidade v 0 . Determine o valor de que maximize a distância horizontal que a bol
Uma esfera A de 1k g é solta de uma altura de 5,909m sobre uma placa B de 2k g , que é suportada por um conjunto acondicionado de molas e que inicialmente está em repouso. Sabendo que o conjunto de mo
Uma bola bate no chão em A com uma velocidade v 0 de 16m / s a um ângulo de 60 ° com a horizontal. Sabendo que e = 0,6 entre a bola e o chão e que após o rebote a bola alcança o ponto B com uma veloci
O pino B de 100 g desliza ao longo da fenda no braço rotativo OC e ao longo da fenda DE, que é cortada em uma placa horizontal fixa. Negligenciando o atrito e sabendo que a haste OC gira a uma taxa co
Um volante de 2.000 kg com raio de giração de 700 mm é deixadolivre a partir de uma velocidade angular de 450 rpm. Sabendo que oatrito cinético produz um binário de intensidade de 16 N m, determine o