Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 36

Uma plataforma circular horizontal tem uma massa de 150 kg e um raio de giraçao k z = 2,4   m em relação ao eixo z passando pelo seu centro O. A plataforma está livre para girar em torno do eixo z e está inicialmente em repouso. Um homem com uma massa de 75 kg aremessa um bloco de 7,5 kg da borda da plataforma com uma velocidade horizontal de 1,5 m/s, medida em relaçao à plataforma. Determine a velocidade angular da plataforma se o bloco é arremessado (a) tangente à plataforma, ao longo do eixo +t, e (b) para fora ao longo de uma linha radial, ou eixo +n. Despreze a dimensão do homem.

Passo 1

Começaremos o exercício analisando a velocidade absoluta do bloco com o auxílio da imagem a seguir:

+ →   v b = v p + v b / p

v h = - 3 ω + 1,5

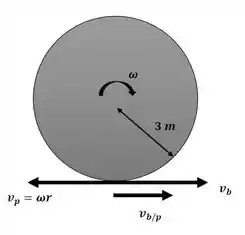
Passo 2

Com isso, podemos aplicar o conceito de conservação da quantidade de movimento angular para o sistema do caso (a):

H 1 z = H 2 z

0 + 0 = 7,5 v b 3 - 150 2,4 2 ω - 75 3 ω 3

v b = 68,4 ω

Agora, igualando esse resultando a equação obtida no passo 1 podemos determinar a velocidade angular da plataforma:

- 3 ω + 1,5 = 68,4 ω

ω = 0,021   r a d / s

Passo 3

Agora, aplicaremos a conservação da quantidade de movimento para o caso (b):

H 1 z = H 2 z

0 + 0 = 0 - 150 2,4 2 ω - 75 3 ω 3

ω = 0

Resposta

ω = 0,021   r a d / s

ω = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola A de 600g move-se com velocidade de 6m / s de intensidade quando é atingida por uma bola B de 1k g que tem velocidade de 4m / s de intensidade. Sabendo que o coeficiente de restituição é 0,8
Dois discos deslizam sobre um plano horizontal sem atrito com velocidades de sentidos opostos e de mesma intensidade v 0 e batem de frente. Sabe-se que o disco A tem uma massa de 3k g e observa-se que
Em uma fornecedora de peças de automóvel, pacotes são transportados para o terminal de carga sendo empurrados ao longo de uma esteira de roletes com muito pouco atrito. Sem instantâneo na figura, os p
O cursor C pesa 230 g e pode mover-se na fenda aberta no braço AB, que gira a uma taxa constante 0,10 rad /s no plano horizontal. O cursor é preso a uma mola de constante k= 36 N/m, que não está defor
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se movimenta sob a ação de uma força central F ao longo de uma trajetória semicircular de diâmetr