Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 41

Os elementos AB e BC da treliça mostrada são feitos da mesma liga. Sabe-se que uma barra quadrada de 20 mm de lado feita do mesmo material foi ensaiada até falha e que uma carga final de 120 kN foi registrada. Se a barra AB tiver uma área de seção transversal de 225 mm² determine A) o fator de segurança para a barra AB e b) a área de seção transversal da barra AC se tiver o mesmo fator de segurança que a barra AB

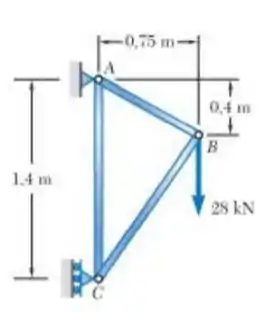
Passo 1

E ai gurizada tudo belezinha??? Primeiramente vamos analisar o diagrama de corpo livre :D

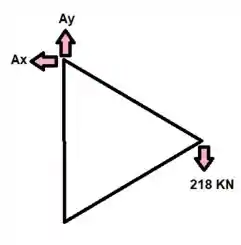
Comprimento do elemento AB:

l a b = 0,75 2 + 0,4 2 = 0,85   m

Use uma treliça inteira como um corpo livre.

+ ↺ ∑ M c = F × d = 0

+ ↺ ∑ M c = 1,44   A x - 075 × 28 = A = 15   K N

Calculando o somatório das forças em y

+ ↑ ∑ F y = 0  

A y - 28 = 28   K N

Passo 2

Gurizada agora devemos desenhar o diagrama de corpo livre para a articulação A:

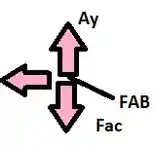
Realizando o somatório das forças em x temos:

+ ∑ F x = 0  

0,75 0,85 F A B - A x = 0

F A B = 0,85 × 15 0,75 = 17   K N

Realizando o somatório das forças em y temos:

+ ↑ ∑ F y = 0  

A y - F a c - 0,4 0,85 F a b = 0

F a c = 28 - 0,4 × 17 0,85 = 20   K N

Passo 3

Calculando a área temos:

A = 0,02 2 = 400   × 10 - 6   m 2

P U = 120 × 10 3   N

Calculando a tensão temos:

σ = P u A

σ = 120 × 10 3 400 × 10 - 6   = 300   M P a

  1. Calculando o fator de segurança para o elemento AB:

    2. F S = 300 × 10 6 × 225 × 10 - 6 17 × 10 ³ = 3,97

     

  2. Calculando o fator de segurança para o elemento AC:

A = 3,97 × 20 × 10 3 300 × 10 6 = 264,67 × 10 - 6   m 2

Resposta

  1. 3,97
  2. 264,67 × 10 - 6   m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quatro vigas de 4,5m suportam uma carga de 21,5k N / m e são apoiadas, como mostrado, em uma longarina A D e em paredes de concreto. Sabendo-se que σ a d m = 140M P a e τ a d m = 90M P a , selecionar
Dois perfil de aço, em forma de cantoneira, L102 × 76 , são perfeitamente unidos para suportar o carregamento mostrado. Sabendo-se que σ a d m = 140M P a e τ a d m = 85M P a , determinar a mínima espe
Para a viga e o carregamento mostrado, determinar a máxima tensão normal nos pontos a ,b e c .
Para a viga e o carregamento mostrado, determinar a máxima tensão de cisalhamento nos pontos a ,b e c .
A viga A B tem uma seção transversal retangular de largura b constante e a altura h variável. Sabendo-se que a viga deve ser de resistência constante, expressar h , em termos de x ,L e h 0 .