Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 94
Para a viga com o carregamento mostrado, dimensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a e .
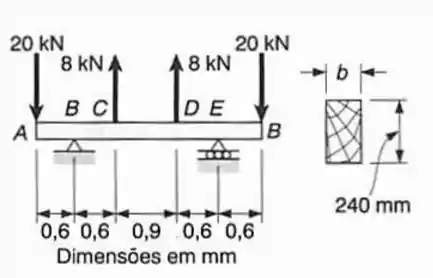
Passo 1
Oi, fala aí, galerinha!!! Para resolver esse problema a gente vai seguir o seguinte passo a passo:
- Calcular as reações em e E, por meio das equações da estática.
- Calcular a força cortante, o momento fletor e achar o momento fletor máximo.
- Calcular o módulo resistente da seção .
- Utilizar o momento fletor máximo o módulo resistente da seção e a máxima tensão admissível para achar o comprimento .
Passo 2
Para facilitar fazer fazer um desenho das forças:
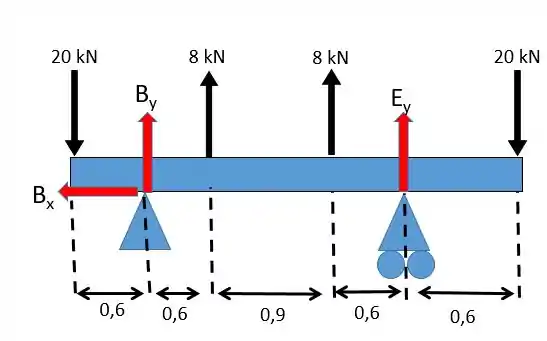
Aplicando a equação de equilíbrio em relação à horizontal vamos ter:
Não há forças na vertical.
Como o problema é simétrico então as forças devem ser iguais, portanto:
Passo 3
Nós queremos o máximo momento fletor máxima, que ocorre exatamente na metade da barra (por ela possuir um carregamento simétrico) assim, Além disso a força cortante é zero nesse ponto então:
Passo 4
Com isso a gente pode achar o valor da tensão cisalhante normal máxima da fora:
Mas a gente não vai fazer essa conta direto, vamos utilizar uma propriedade chamada de módulo resistente da seção , que é dada por:
Ou seja, o momento de inércia sobre a maior distância até a linha neutra . Vamos calcular esse ?
Assim:
Reorganizando:
Vamos guardar esse valor porque isso é importante!
Passo 5
Agora vamos substituir na equação da tensão normal:
Perceba que como
Então:
Aí aqui a gente vai fazer o négocio um pouco diferente. Se lembra que eu disse que o era importante? Então, agora que vamos utiliza-lo porque a equação acima pode ser escrita como:
Agora é só substituir os valores que a gente já achou!
Aqui podemos utilizar o momento fletor em módulo:
Porém isso não é o bastante =(
A gente tem que ver se o carregamento não faz a estrutura falhar por cisalhalhamento.
Passo 6
Para fazer essa análise a gente vai utilizar a aproximação para seções retangulares:
A gente pode achar o que ocorrerá entre A e B:
Substituindo os valores
Então a dimensão de deve ser mesmo igual a