Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 148
A polia e a engrenagem estão submetidas às cargas mostradas. Para estar forças, determine o sistema força-binário equivalente no ponto .
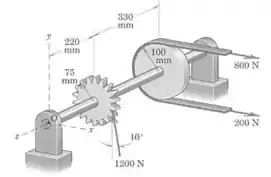
Passo 1
Vamos começar escrevendo a força de em forma vetorial:
Agora podemos calcular a força resultante:
Passo 2
Falta calcular o momento gerado por essas forças. A rotação das engrenagens gera um momento em torno do eixo , já que é em torno desse eixo que elas giram. Vamos então calcular essa componente.
Começamos pelas duas forças que agem sobre a polia de raio . Como as forças favorecem a rotação em sentidos contrários, o momento total é o seguinte:
E agora vamos ver o momento da força que age sobre a engrenagem de raio :
E a outra componente da força não gera momento porque sua linha de ação passa pelo centro da engrenagem.
Então na direção do eixo temos:
Passo 3
Além disso, as componentes das forças no sentido do eixo geram momento em torno do eixo , então:
Onde o sinal negativo aparece porque essas duas forças favorecem a rotação no sentido horário.
E então:
Passo 4
Finalmente, as componentes na direção do eixo favorecem a rotação em torno do eixo :
E nesse caso só vamos considerar a força de , já que as outras duas não geram momento nessa direção.
E então:
Agora podemos calcular o momento total:
Resposta
A força é e o momento é .