Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 152
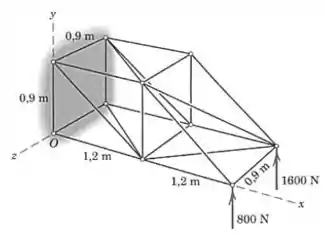
Duas cargas direcionadas para cima são exercidas sobre uma pequena treliça tridimensional. Reduza estas duas cargas a um único sistema força-binário no ponto . Mostre que é perpencidular a . Em seguida, determine o ponto no plano - pelo qual passa a resultante.
Passo 1
Começamos calculando a força resultante:
Então:
Passo 2
Agora vamos calcular os momentos das forças.
A força de gera momento apenas em torno do eixo :
E a força de gera momento em torno dos eixos e :
E então:
Passo 3
Agora vamos verificar se e são perpendiculares. Para isso temos que calcular o produto interno:
Como o produto é zero, podemos garantir que os dois vetores são perpendiculares.
Passo 4
Agora queremos saber em qual ponto no plano - passa a força resultante. Temos que escolher esse ponto de forma que o momento total seja o mesmo.
E o momento que calculamos antes era:
Então:
Resposta
A força resultante é , o momento total é e esses dois vetores são perpendiculares. As coordenadas são e .