Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 15
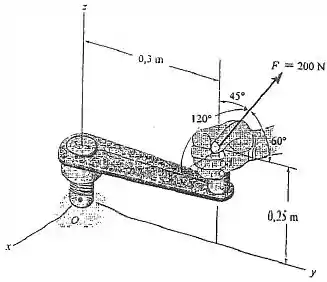
15. Determine a intensidade do momento da força de em relação ao eixo x.
Passo 1
Para resolver esse exercício vamos o método de análise escalar que é baseada na fórmula:
Onde d nesse caso é a distância perpendicular do braço do momento a parti do eixo da linha da força.
Nessa situação teremos que decompor nossas forças em relação aos eixos coordenados.
A componente da força que é paralela ao eixo x que vai ser no caso a componente x da força, não produz qualquer momento ou tendência para girar em torno desse eixo.
Assim as duas componentes que importam é e .
Vamos definir também o sentido positivo do momento conforme a regra da mão direita.
Passo 2
Vamos calcular as componentes da força .
Passo 3
Temos que os braços de momento referentes a cada força e que são perpendiculares a linha de ação de sua respectiva componente da força são:
Assim nosso momento em relação ao eixo de rotação x é:
A primeira componente é negativa pois faz com que o objeto rode no sentido horário em relação ao eixo x.
Continuando:
Resposta
A intensidade do momento da força é: