Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 132
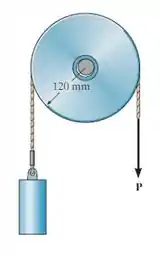
A polia de tem um diâmetro de e o eixo tem um diâmetro de . Se o coeficiente de atrito cinético entre o eixo e a polia , determine a força vertical na corda necessária para levantar o bloco de em velocidade constante.
Passo 1
Lá da teoria de atrito, temos que o momento necessário para manter a rotação constante do eixo pode ser encontrado somando os momentos em relação ao eixo do eixo motor, ou seja, ;
onde é o ângulo de atrito cinético definido por . Pela figura abaixo, vemos que . O círculo tracejado com raio é chamado de círculo de atrito, e à medida que o eixo gira, a reação sempre será tangente a ele.
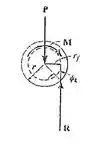
Se o mancal for lubrificado, será pequeno, e, portanto, . Assim, podemos escrever o raio do círculo de atrito como .
Passo 2
Portanto, para o eixo da polia vamos ter o seguinte raio do círculo de atrito:
Passo 3
Para todo sistema em equilíbrio, o somatório dos momentos em relação a um ponto é igual a zero. Assim, assumindo como sentido positivo o anti-horário temos:
Resposta
O valor da força vertical deve ser: