Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 116

Se a mola exerce uma força de 4500   N sobre o bloco determine o torque M necessário para girar o eixo. O coeficiente de atrito estático em todas as superfícies de contato é μ s = 0,3 .

Passo 1

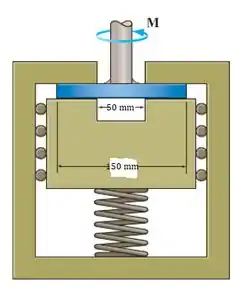
Nessa questão temos um mancal de escora, onde precisamos encontrar o torque necessário para superar a força de atrito. O mancal de escora no eixo mostrado abaixo está sujeito a uma força axial P e tem uma área total do mancal ou de contato π R 2 2 - R 1 2 . Desde que o mancal seja novo e uniformemente apoiado, então a pressão normla p sobre o mancal será distribuído uniformemente sobre essa área. Como ∑ F z = 0 , então p , medido como uma força por unidade de área é p = P π R 2 2 - R 1 2 .

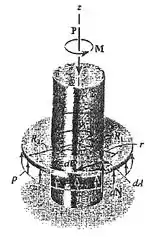
O momento necessário para causar iminência de rotação do eixo ser determinado a partir do equilíbrio de momento em relação ao eixo z . Um elemento diferencial de área d A = ( r d θ ) ( d r ) está sujeito a uma força normal d N = p d A e uma força de atrito associada,

d F = μ s d N = μ s p d A = μ s P π R 2 2 - R 1 2 d A

A força normal não cria um momento em relação ao eixo z do eixo motor; porém a força de atrito cria; a saber, d M = r d F . A integração é necessária para calcular o momento aplicado M necessário para superar todas as forças de atrito. Portanto, para iminência de movimento rotacional,

∑ M z = 0

M - ∫ A a r d F = 0

Substituindo por d F e d A e integrando sobre a a´rea inteira do mancal, temos:

M = ∫ R 1 R 2 ∫ 0 2 π r μ s P π R 2 2 - R 1 2 r d θ d r = μ s P π R 2 2 - R 1 2 ∫ R 1 R 2 r 2 d r ∫ 0 2 π d θ

M = 2 3 μ s P R 2 3 - R 1 3 ( R 2 2 - R 1 2 )

Passo 2

Vamos agora aplicar os valores da questão na equação encontrada acima! Temos que R 1 = 50 2 = 25   m m e R 2 = 150 2 = 75   m m , μ s = 0,3 e P = 4500   N . Como M é requerida para superara a força de atrito das duas superfícies de contato, temos:

M = 2 2 3 μ s P R 2 3 - R 1 3 R 2 2 - R 1 2

M = 2 2 3 ( 0,3 ) 4,5 × 10 3 75 × 10 - 3 3 - 25 × 10 - 3 3 75 × 10 - 3 2 - 25 × 10 - 3 2

M = 146,25   N m

Resposta

O torque necessário para girar o eixo é:

M = 146,25   N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os blocos de 10 kg e de 25 kg estão presos por uma corda pendurada sobre a superfície curva fixa. Se o sistema está no limiar de escorregar, calcule o coeficiente de atrito entre a corda e a superfíci
Um marinheiro ajusta uma corda que impede que um barco se desloque ao longo de uma doca. Se ele puxa com uma força de 200 N a corda que está enrolada 1 ¼ de volta no mourão, que força T ele conseguirá
Determine a força P necessária para ( a ) levantar e ( b ) abaixar o cilindro de peso W a uma velocidade constante baixa. O coeficiente de atrito entre a corda e o eixo fixo vale 0,4.
Observa-se que os dois cilindros permanecem em movimento lento e constante, como indicado na figura. Determine o coeficiente de atrito μ entre a corda e o eixo rígido.
Com que força horizontal P o trabalhador deve puxar para mover a tora de 35 kg para cima na inclinação com 15°? O coeficiente de atrito entre a tora e a inclinação vale 0,60 e entre a corda e a rocha