Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 96
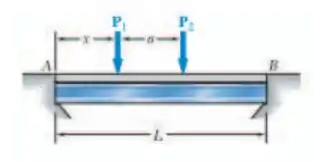
Uma ponte de comprimento deve ser construída em uma estrada secundária cujo acesso a caminhões está limitado a veículos de dois eixos de peso médio. Ela consistirá em uma laje de concreto e vigas de aço simplesmente apoiadas com um limite de resistência . O peso combinado da laje e das vigas pode ser aproximado por uma força uniformemente distribuída em cada viga. Para as finalidades do projeto, considera-se que um caminhão com distância entre eixos de passará pela ponte e que as forças concentradas resultantes e exercidas em cada viga serão de até e , respectivamente. Determine o perfil de mesas largas mais econômico para as ficas, usando a LRFD com os coeficientes de carga , e coeficiente de resistência . [Sugestão: Pode-se mostrar que o valor máximo ocorre sob a força maior quando a força está localizada à esquerda do centro da viga a uma distância igual a .]
Passo 1
Fala aí, pessoal. Beleza? Bora zerar esse livro.
Este problema nos pede para selecionar o perfil mais econômico que suporta o carregamento dado. Primeiro, bora esboçar o DCL para as vigas e:
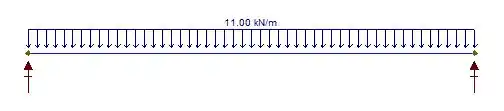
Sabendo disso, vamos calcular a reação de apoio através das equações de equilíbrio:
Por simetria, temos que , logo:
Assim, podemos concluir esboçar o diagrama força cortante:
E também o diagrama de momento fletor:
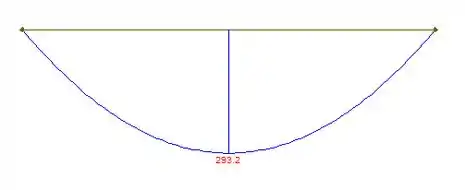
Assim, podemos ver que o momento máximo absoluto é:
Passo 2
Em seguida, vamos utilizar a equação que o enunciado deu pra gente, para determinarmos a distância que é a distância à esquerda do centro da viga na qual a força vai agir. Logo:
Portanto:
Já a força de maior intensidade, vai agir na posição:
Essas posições em que as forças e estarão agindo.
Passo 3
Agora que determinamos a posição onde as força vão agir, podemos esboçar seu DCL, temos:
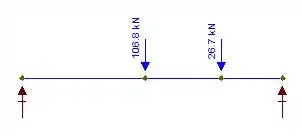
Em seguida, vamos calcular a reação de apoio através das equações de equilíbrio:
E também:
Portando:
Assim, podemos esboçar o diagrama força cortante:
E também o diagrama de momento fletor:
Assim, podemos ver que o momento máximo absoluto é:
Passo 4
Agora, para encontrarmos o perfil de mesas largas mais econômico vamos utilizar o método LRFD, que é dado por:
Onde é o valor mínimo admissível do módulo de resistência da seção da viga. Subsituindo:
Assim, vamos até o ábaco do nosso livro para encontrar o valor mínimo admissível do módulo de resistência imediamente maior que que encontramos. Portanto, o perfil escolhido é:
Que possui .
É isso, galera! Bora fazer mais exercícios pra ficar craque.