Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 115

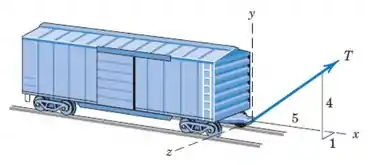
Uma ponte rolante é usada para reposicionar o vagão dentro de uma oficina de reparos para vagões. Se o vagão começa a mover-se ao longo dos trilhos, quando a componente  x  da tensão do cabo alcança 3   k N , calcular a tensão necessária  T  no cabo. Determinar o ângulo  θ x y  entre o cabo e o plano vertical  x - y .

Passo 1

E aí meus queridxs, tudo bem com vocês?

Se liguem só que essa questão é bem rapidinho, mas exige um pouco da nossa atenção para que não fiquemos perdidos. Primeiramente, devemos nos lembrar que o enunciado nos diz que a componente x da força vale 3 k N , ou seja,

T x = 3 k N

Mas nós devemos saber também que T x pode ser escrito como

T x = T ⋅ cos ⁡ θ

Onde nosso cos ⁡ θ vai ser dado por

cos ⁡ θ = 5 41     ( v e r   o   t r i â n g u l o   f o r m a d o   n a   f i g u r a )

Pois bem, com essas duas expressões nós podemos escrever o seguinte

T x = T x

Então, teremos

T ⋅ cos ⁡ θ = 3 k N → T = 3 k N ⋅ 41 5 ≈ 3,8 k N

n a b = 0,77 i + 0,62 j + 0,15 k

Passo 2

Primeira parte do nosso problema tá resolvida. Vamos agora escrever o vetor O T fazendo

O T → = 5 - 0 i + 4 - 0 j + 1 - 0 k

O T → = 5 i + 4 j + k

Assim, nosso ângulo formado entre esse vetor e nosso plano x - y será dado por

θ = a r c o s   5 2 + 4 2 5 2 + 4 2 + 1 2

θ = arccos ⁡ 0,9 88 ≈ 8 , 88 °

Pronto, tá resolvido nosso problema.

Resposta

T = 3,8 k N ,   θ x y = 8,88 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força F atua ao longo da linha M A , em que M é o ponto médio do raio ao longo do eixo x . Determine o sistema força-binário equivalente no ponto O , se θ=40 ° .
Os pontos AeB são os pontos médios dos lados do retângulo. Substitua a forçaF dada atuando em A por um sistema força-binário em B .
Determine o sistema força-binário equivalente na origem O para cada um dos três casos de forças sendo aplicadas nas arestas de um hexágono regular de largura b . Substitua esse sistema força-binário p
Sob condições não uniformes e escorregadias da estrada, as duas forças mostradas são exercidas sobre as duas rodas de tração traseiras da caminhonete, que tem um diferencial traseiro que limita derrap
Ao empurrar uma mesa na direção da porta de saída, três estudantes exercem as forças mostradas na vista de topo. Determine o sistema força-binário equivalente no ponto A . Determine, então, a equação