Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 96

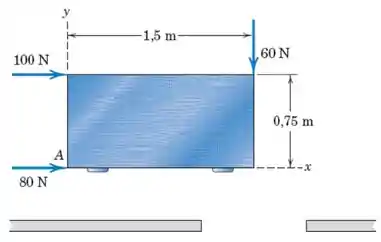
Ao empurrar uma mesa na direção da porta de saída, três estudantes exercem as forças mostradas na vista de topo. Determine o sistema força-binário equivalente no ponto . Determine, então, a equação da linha de ação da força resultante.

Passo 1

E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?

Prestem bastante atenção que essa questão é relativamente rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não se perca no meio do caminho. Primeiramente, vamos escrever as três forças presentes na figura em forma vetorial, de modo que obtemos

Dessa forma, teremos como resultante a soma dessas três forças e será dada por

Sem mudar o efeito que já tínhamos no problema, desejamos substituir essas três forças por um binário em . Para isso, vamos ter além da força um binário em que chamaremos de

Passo 2

Adotando como positivo o sentido anti-horário vamos ter que nosso binário será dado por

O sinal negativo nos indica que nossa tendência de giro é no sentido horário. Pronto, já temos o sistema força-binário pedido pelo enunciado.

Passo 3

Por fim, para concluirmos nosso exercício precisamos encontrar a linha de ação da força resultante. A força tem que ser aplicada em um ponto que mantenha o momento total das forças sobre o sistema obedecendo a

Onde é o vetor do momento das forças em relação a e é o vetor posição do ponto onde a força será aplicada. Pela regra da mão direita como a rotação está no sentido horário, o vetor aponta no sentido que entra no plano. Dessa forma, teremos