Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 78

A força  F   atua ao longo da linha  M A , em que  M  é o ponto médio do raio ao longo do eixo  x . Determine o sistema força-binário equivalente no ponto  O , se  θ   =   40 ° .

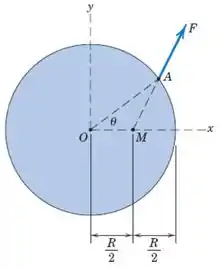
Passo 1

E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?

Prestem bastante atenção que essa questão é relativamente rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não se perca no meio do caminho. Pois bem, para nos ajudar na resolução desse exercício tomemos a seguinte construção geométrica

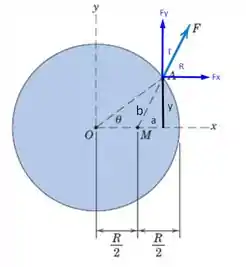
Da figura podemos inferir que

y = R ⋅ s e n 40 ° = 0,6428 R   b = y 2 + a 2 = 0,6957 R   h = R 2 + a = R ⋅ cos ⁡ 40 ° = 0,766 R a = R ⋅ cos ⁡ 40 ° - 1 2 = 0,266 R T = a r c s e n   a b ≈ 22,48 °

Com esses dados podemos encontrar o ângulo de ação da nossa força que será dado por

R = 90 ° - T = 90 ° - 22,48 ° = 67,5 °

Passo 2

Agora que fizemos, essa construção podemos calcular nossas componentes da nossa força que serão dadas por

F x = F ⋅ cos ⁡ 67,5 ° ,     F y = F ⋅ s e n 67,5 °

Com isso vamos ter o seguinte momento (adotando o sentido anti-horário como positivo)

M 0 = F y ⋅ h - F x ⋅ y = F ⋅ s e n 67,5 ° ⋅ 0,766 R - F ⋅ cos ⁡ 67,5 ° ⋅ 0,6428 R

M 0 = 0,462 F R   s e n t i d o   a n t i   h o r á r i o

Pronto, está resolvido nosso problema.

Resposta

F   a   67,5 ° ,   M 0 = 0,462 F R   s e n t i d o   a n t i   h o r á r i o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado quando os crankpins de um motor de dois cilindros passam pelo plano horizontal y - z , a haste A está sob uma compressão de 1,8k N e a haste B está sob uma compressão de 0,8k N .
A força de 180l b é aplicada no ponto A do suporte. Determine os momentos desta força sobre o ponto B, sobre o ponto C e sobre a linha B C - .
Substitua as duas forças e o binário simples por um sistema de força-binário equivalente no ponto A.
O topo horizontal de um pilar de concreto está sujeito ao sistema de forças mostrado. Represente a resultante de todas as forças como uma força R → no ponto O e um binário M → . Também especifique as
Duas cargas ascendentes são exercidas na pequena treliça tridimensional. Reduza essas duas cargas a um único sistema de força-binário no ponto O. Mostre que R → é perpendicular a M O → . Em seguida, d