Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 86
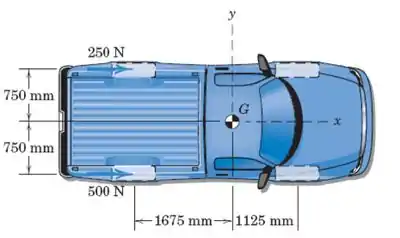
Sob condições não uniformes e escorregadias da estrada, as duas forças mostradas são exercidas sobre as duas rodas de tração traseiras da caminhonete, que tem um diferencial traseiro que limita derrapagens. Determine a interseção com o eixo da resultante desse sistema de forças.
Passo 1
E aí meus queridxs, tudo bem com vocês? Espero que sim. Se liguem só, primeiro de tudo vamos escrever nossas duas forças em forma vetorial, assim, teremos
Sendo assim, nosso vetor força resultante, , pode ser calculado apenas somando as duas forças de modo a obtermos
Passo 2
Queremos preservar nosso momento do estado inicial, , com relação ao ponto . Sendo assim, adotando o sentido anti-horário como positivo poderemos calcular esse momento fazendo
Para que nossa força produza esse mesmo momento, a posição dela no eixo vai ter que satisfazer a seguinte equação
Só que devemos nos atentar ao seguinte: a conta que acabamos de efetuar está sendo feita toda em módulo, então, devemos verificar nosso resultado para saber se a posição de aplicação da nossa força resultante está acima ou abaixo do ponto . Como adotamos que o sentido anti-horário é positivo, podemos observar pela imagem que para que nossa força produza uma rotação nesse sentido, devemos ter que a posição de atuação dela está abaixo do ponto ou seja
Pronto, está resolvido nosso problema.