Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 56

5.56. Determine the y-coordinate of the centroid of the shaded area.

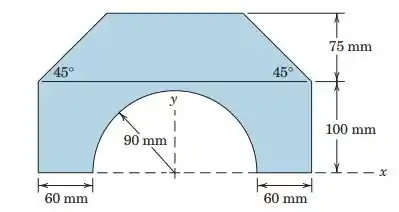
Passo 1

Vamos em busca de mais um centroide!

Essa figura é um pouco complicada para calcular o centroide, por isso vamos separar em várias figuras mais fáceis de calcular:

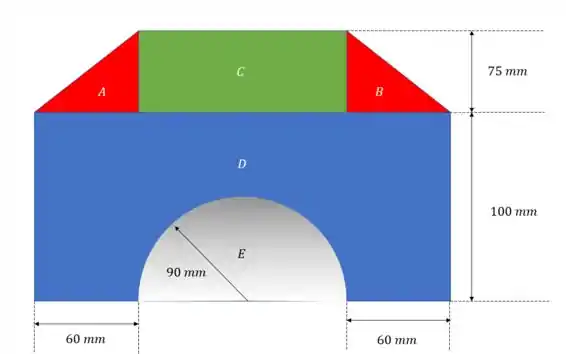
Então temos cinco figuras, dois triângulos, dois retângulos e um semicírculo, mas atenção, o semicírculo é como se fosse uma parte faltando na figura, então tudo que calcularmos relacionado a essa parte da figura vamos usar o valor negativo.

Passo 2

Vamos começar os cálculos, podemos começar com os triângulos A e B , eles são perfeitamente simétricos, então a suas áreas vão ser idênticas e o centroide em y também vai ser idêntico.

Vamos começar pela área:

A A = A B = b ⋅ h 2

A gente consegue ver a altura de primeira, mas a base não está clara. Mas a gente sabe que o ângulo entre os catetos é 45 ° , e isso significa que b = h .

A A = A B = 75 2 2 = 2812,5   m m 2

Agora vamos calcular o centroide. Vai ficar mais fácil se mudarmos o centro do sistema de coordenadas.

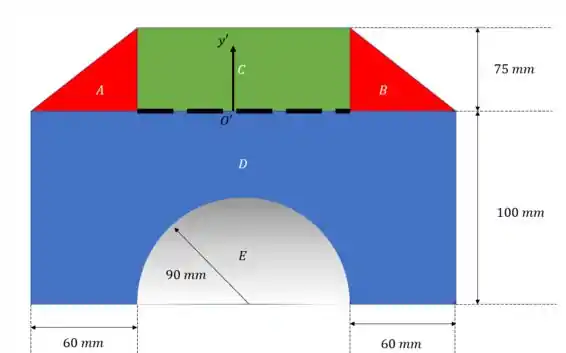
O novo centro O ' está no ponto y = 100

Agora podemos fazer:

y - A ' = y - B ' = h 3 = 75 3 = 25   m m

Agora vamos passar paras o centro original das coordenadas.

y - = y - ' + O '

Então

y - A ' = y - B ' = 25 + 100 = 125   m m

Passo 3

Agora vamos para o retângulo de cima, o retângulo C , em verde.

Vamos começar bela área

A C = b ⋅ h

De novo é fácil ver o valor da altura, mas a base é um pouco complexa. Bom, podemos dizer que a base do trapézio formado pelos dois triângulos e o retângulo é:

b T = 60 + 60 + 90 ⋅ 2 = 300   m m

Agora para pegar só a parte do retângulo, podemos subtrair os valores das bases dos triângulos:

b = 300 - 2 ⋅ 75 = 150   m m

Então a área é:

A C = 150 ⋅ 75 = 11250   m m 2

Agora vamos calcular o centroide, e para isso podemos usar o mesmo centro O ' que usamos para calcular o centroide dos triângulos:

y - C ' = 75 2 = 37,5   m m

Agora no sistema de coordenadas originais:

y - C = 100 + 37,5 = 137,5   m m

Passo 4

É a vez do retângulo D . Esse aqui vai ser rapidinho.

A D = b ⋅ h = 300 ⋅ 100 = 30000   m m 2

Agora vamos ver como fica o centroide.

y - D = 100 2 = 50   m m

Passo 5

Só falta o semicírculo agora.

Vamos começar pela área:

A E = 1 2 π r 2 = 1 2 π 90 2 = 12723,45   m m 2

Agora vamos ver como fica o centroide.

y - E = 4 3 r π = 4 3 90 π = 38,20   m m

Lembrando que esse semicírculo é uma parte que está fora da figura, então esses resultados serão negativos.

Passo 6

Agora vamos calcular o centroide da figura completa:

y - = ∑ A y - ∑ A  

Isso fica

y - = A A y - A + A B y - B + A C y - C + A D y - D - A E y - E A A + A B + A C + A D - A E

Agora vamos substituir esses valores

y - = 2 2812,5 ⋅ 125 + 11250 ⋅ 137,5 + 30000 ⋅ 50 - 12723,45 ⋅ 38,20 2 2812,5 + 11250 + 30000 - 12723,45

Fazendo essa conta toda aqui ficamos com

y - = 95,57   m m

Resposta

y - = 95,57   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o centroide z da figura:
Determine o centróide da em z da figura abaixo.
With your pencil, make a dot on the position of your best visual estimate of the centroid of the area of the circular sector. Check your estimate by using the results of Sample Problem 5/3.
Specify the x-, y-, and z-coordinates of the mass center of the homogeneous semicylinder.
With your pencil, make a dot on the position of your best visual estimate of the centroid of the triangular area. Check the position of your estimate by referring to the results of Sample Problem 5/2