Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 32
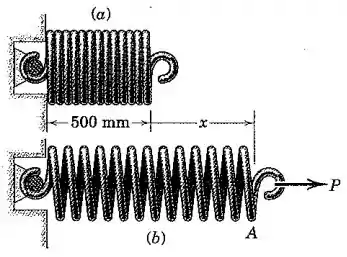
Na posição não esticada as espiras da mola de estão quase tocando uma na outra, como mostrado na parte (a) da figura. Na posição esticada a força , proporcional a , é igual a quando . Se a extremidade da mola é liberada bruscamente, determine a velocidade da espira na extremidade , medida positiva para a esquerda, conforme se aproxima da sua posição não esticada em . O que acontece com a energia cinética da mola?
Passo 1
Perceba que é fisicamente impossível que a mola adquira um comprimento menor do que , então quando , não pode haver velocidade na mola, e portanto, a energia cinética é nula. Porém, quando , ou seja, quando a mola está quase chegando ao seu comprimento-limite, a extremidade ainda tem velocidade, pois toda a energia potencial da mola de antes se transforma em energia cinética, pela conservação da energia mecânica:
Então, vamos calcular quando :
Passo 2
Para calcular a energia cinética quando , temos que lembrar que cada pedaço da mola tem que se mover com uma velocidade proporcional à sua distância da extremidade esquerda da mola, ou seja:
onde e correspondem a um ponto qualquer da mola. Sabendo disto, podemos escrever a integral que nos dá a energia cinética:
No entanto, vimos que:
Além disso, podemos expressar como função de , ao calcular a densidade linear da mola:
Passo 3
Logo, podemos reescrever a integral assim:
Porém, lembre-se de que :
Então, quando , a velocidade da extremidade é , mas quando , essa velocidade se anula bruscamente, porque a mola não pode se comprimir, então toda a energia cinética se dissipa, em calor, som etc.
Resposta
A energia cinética se dissipa, em calor, som etc.