Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 225
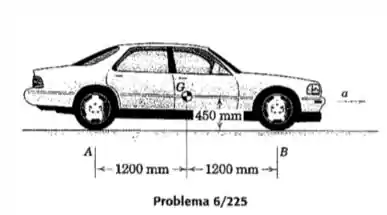
O carro com tração nas rodas traseiras possui uma massa de 1600 kg com centro de massa em . O coeficiente de atrito efetivo entre os pneus e a estrada é de . considere o carro e as rodas como um único corpo rígido, desprezado a inercia rotacional das rodas e calcule a aceleração máxima que o carro é capaz de atingir. Em seguida, calcule o torque aplicado em cada roda por seu eixo. Cada roda traseira tem uma massa de 32 kg. Um diâmetro de 620 mm e um raio de giração de 210 mm.
Passo 1
A aceleração pedida na letra (a) será máxima quando a força sobre as rodas traseiras, que possuem tração, for dada somente pela força de atrito:
Designaremos para a força normal aplicada sobre o ponto A, que se encontra exatamente no contato entre a roda traseira e o chão, e para o ponto de contato entre a roda dianteira e o chão.
Passo 2
Agora vamos considerar um terceiro ponto C, que se encontra na mesma linha horizontal que passa pelo ponto G, e na mesma linha vertical que passa pelo ponto B. calculando os momentos em relação a esse ponto teremos:
Os momentos serão o momento da força de atrito, o momento da força peso sobre o centro de massa, e o momento da força normal sobre o ponto A:
Será zero, pois, C pertence à linha do vetor , que deve passar pelo centro de massa.
Isolando :
Substituindo os valores:
E a força de atrito será:
Passo 3
Utilizando a segunda lei de Newton para a coordenada x:
Como a única força atuando sobre o carro no eixo x é a força de atrito:
Passo 4
Para a letra (b), precisamos calcular o momento de inercia para uma das rodas, podemos usar o raio de giração dado no enunciado e o eixo que passa no centro da roda O:
E pela equação da aceleração angular:
Por fim, utilizamos a equação do momento:
Dividimos o momento da força de atrito por 2 por que estamos calculando o momento em uma roda, e não nas duas.
O torque sobre as rodas será: