Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 99
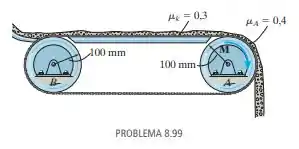
O material granular, com uma densidade de , é movimentado por uma correia transportadora que desliza sobre a superfície fixa, com um coeficiente de atrito cinético de . A correia é acionada por um motor que fornece um torque à roda A. A roda em B está livre para girar, e o coeficiente de atrito estático entre a roda em A e a correia é . Se a correia está sujeita a uma tração pré-tensionadora de quando não está sendo acionada, determine o maior volume V de material permissível sobre ela, a qualquer momento, que não venha travar seu movimento. Qual é o torque M exigido para impulsionar a correia quando ela está sujeita a essa carga máxima?
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiramente, sabemos que a força exercida pelo material é:
Esta é a força normal à superfície. A força de atrito é dada por:
Esta força deve ser no mínimo, igual à força de da correia:
Passo 2
O momento será dado pela força vezes o raio da roda, que é dado por: