Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 62
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de no sentido horário. Determine as velocidades angulares das barras BD e DE.
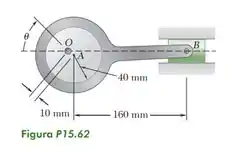
Passo 1
E aí meus caros! Simbora pra mais uma questão do Beer!
Bom! A questão quer que a gente determine a velocidade do bloco quando o sistema faz um determinado ângulo com a horizontal...
Pois muito bem! Pra entender melhor esse problema, a primeira coisa que a gente tem que fazer é um esboço do que está acontecendo... Vamos fazer um desenho, tomando como referências o eixo , o centro e o pino ...
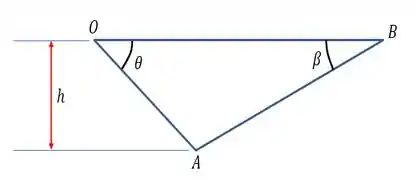
Considerando , e como pontos, eles vão formar um triângulo... E com base na figura acima, podemos estabelecer a seguinte relação abaixo:
E como podemos ver, é o ângulo que forma com a horizontal... Sendo assim, isolando :
Supondo que estamos trabalhando com um ângulo muito pequenininho, vamos considerar que é . Logo, substituindo os valores numéricos;
Passo 2
Continuando nosso raciocínio, a questão afirma pra gente que o disco está girando a uma velocidade angular de . E se o disco rotacional em torno do eixo , então...
Lembrando que o disco está girando, é claro, no sentido horário. Desse modo, podemos determinar a velocidade no centro do disco como igual à...
Passo 3
Em seguida, vamos analisar a distância entre o centro e o pino em .
Bora tomar como referência o plano de movimento para ... O movimento aí é dado basicamente pela soma da translação com e da rotação sobre , mais ou menos o que está exposto na seguinte figura abaixo...
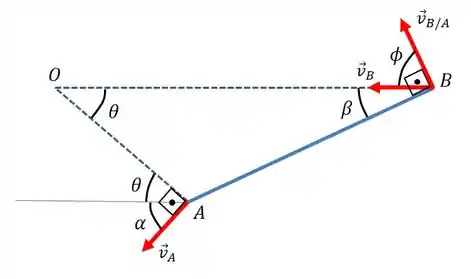
Calculando , temos que...
E depois, é a vez de calcular , que é dado por...
Passo 4
Com esses ângulos calculados anteriormente, podemos montar o seguinte diagrama de velocidades relacionando a velocidade de ), a velocidade do disco ) e a velocidade de em relação a )...
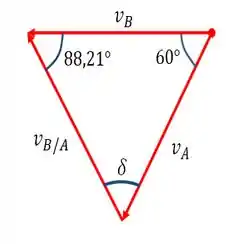
O ângulo é dado por...
Sendo assim, com base na lei dos senos, podemos encontrar :
Como ...