Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 81

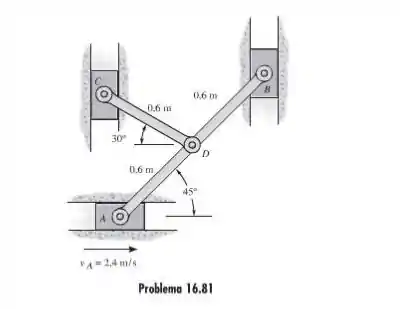
81. Se o bloco deslizante A está se deslocando para a direita a v A = 2,4   m / s , determine a velocidade dos blocos B e C no instante mostrado. O membro CD está conectado por pino ao membro ADB.

Passo 1

Primeiro devemos aplicar a equação da velocidade relativa entre os pontos ADB, assim:

v B = v A + ω A D B × r B / A

v B j = 8 i + ( ω A D B k ) × ( 0,84 i + 0,84 j )

v B j = 8 - 0,84 ω A D B i + 0,84 ω A D B j

Igualando as componentes correspondentes.

0 = 8 - 0,84 ω A D B

v B = 0,84 ω A D B

Resolvendo as equações acima, obtemos:

ω A D B = 2,828   r a d / s

v B = 2,37   m / s

Passo 2

A componente x e y da velocidade do ponto D pode ser obtida a partir de:

v D = v A + ω A D B × r D / A

v D x i + v D y j = 8 i + 2,828 k × ( 0,43 i + 0,43 j )

A partir daí, obtemos que:

v D x = 1,22 m s

v D y = 1,22   m / s

Aplicando a equação da velocidade relativa entre os pontos C e D, teremos:

v C = v D + ω C D × r C / D

- v C j = 1,22 i + 1,22 j + ω C D k × ( - 0,53 i + 0,3048 j )

A partir daí, obtem-se que:

ω C D = 4 r a d s

v C = 0,89   m / s

Resposta

v B = 2,37   m / s

v C = 0,89   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.88. A roda gira sobre seu cubo sem deslizar na superfície horizontal. Se a velocidade do centro da roda é V c = 0,6 m s , para a direita, determine as velocidades dos pontos A e B no instante mostr
16.95. A roda está rigidamente fixada à engrenagem A , que está engrenada às cremalheiras D e E . Se D tem uma velocidade V D = 1,8m / s e V E = 3 m / s . Demonstre que é necessário que a roda deslize
72. O trem de engrenagens epicicloidal consiste da engrenagem sol A que está engrenada à engrenagem planetária B. Esta tem um cubo interior com a engrenagem C que está fixo em B e engrenado na engrena
73. Se a barra de ligação AB tem uma velocidade angular ω A B = 4r a d / s no instante mostrado, determine a velocidade do bloco deslizante E nesse instante. Também identifique o tipo de movimento de
16.106. A placa quadrada está restringida dentro das ranhuras em A E B . Quando θ = 30 ° , o ponto A está se deslocando com V A = 8 m s . Determine a velocidade do ponto C nesse instante.