Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 116
O apoio axial está sujeito a uma distribuição de pressão parabólica em sua superfície de contato. Se o coeficiente de atrito estático é , determine o torque necessário para superar o atrito e girar o eixo se ele suporta uma força axial .
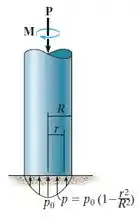
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos que calcular o torque necessário para superar o atrito.
Como nesse caso o eixo está suportando a uma distribuição de pressão, temos que determinar a fórmula para o cálculo do momento, assim como foi feito na seção 8.6.
Então, vamos aos cálculos! O eixo está sujeito a uma força:
O momento será dado por:
E assim chegamos à relação para o torque .
Passo 2
Mas calma! Ainda não terminamos a questão! Para a finalizarmos a questão temos que expressar a pressão em termos de . Para isto, basta integrarmos a força que explicitamos no Passo anterior.
Portanto,
E para finalizarmos, basta substituir na relação do torque .
E assim finalizarmos a questão!