O poste é feito de alumínio e tem de diâmetro. Está preso aos suportes e e em seu centro há uma mola espiral acoplada ao colar rígido. Se a mola não estiver comprimida na posição inicial, determine a compressão na mola quando a carga for aplicada ao colar.

Primeiro temos que entender melhor como o poste está se deformando. Vamos pegar uma seção acima de e uma seção abaixo de .

A força puxa para baixo, então dois efeitos irão ocorrer:

• A seção superior () sofre uma tração, alongando um comprimento .
• A seção inferior () sofre uma compressão, diminuindo um comprimento .

Queremos esse . Pela fórmula da relação carga-deslocamento temos

A área a gente consegue calcular, e já temos. Só falta descobrir a força então!

Com as seções cortadas em , as forças ficam como na figura.

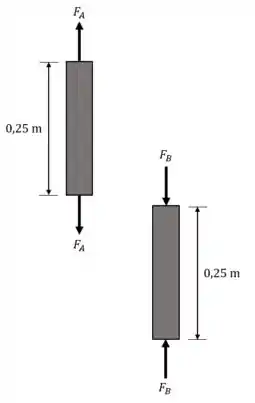
Então para o deslocamento da metade inferior () precisamos de !

Aí você já sabe. Procurando força = diagrama de corpo livre.

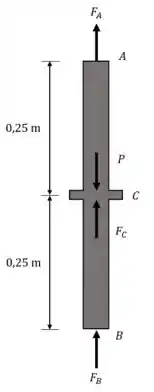
Condição de equilíbrio:

A força é desenvolvida pela mola. Ela depende de o quanto a metade inferior do poste é comprimido:. Usando a relação linear de uma mola:

O a gente já sabe que está relacionado a por:

Então,

Duas incógnitas e uma equação. Vamos manter nosso plano de achar primeiro procurando por mais uma equação com a condição de compatibilidade.

Agora vem o grande macete desses exercícios. O poste está entre duas paredes rígidas! Então ele não pode ultrapassar elas. O resultado dos dois efeitos (aumentar e diminuir) tem que ser zero:

Pronto, só usar essa relação na equação de equilíbrio.

Vamos precisar da área do poste: .

Agora é só calcular o !

Usando a fórmula: