Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 8
A carga é sustentada pelos quatro cabos de aço inoxidável conectados aos elementos rígidos e . Determine o deslocamento vertical da carga de se os elementos estiverem na horizontal quando a carga for aplicada. Cada cabo tem área de seção transversal de .
Passo 1
Vamos lá! Respira fundo e vem comigo!
Pois bem, queremos encontrar o deslocamento vertical da carga de mostrada na figura no ponto . Beleza, o que a gente precisa fazer então? Precisamos, então, lembrar que a fórmula a ser usada para que possamos encontrar o deslocamento vertical é a seguinte
Nesse caso, como o material é o o seu módulo de elasticidade é tabelado e dado por .
Aproveitando que estamos colocando aqui nossos dados, bora deixar anotado aqui nossas constantes de acordo com a notação que usaremos:
Passo 2
Vamos achar as forças para cada cabo, beleza? Aí a gente resolve essas barras separadamente, de baixo para cima.
Nós temos que para a barra mais baixa (adotando o sentido anti-horário como positivo)
Para as forças verticais vamos ter
Para a barra mais elevada, também adotando, o sentido anti horário como positivo, vamos ter
De forma análoga ao anterior, para as forças verticais nós teremos
Passo 3
Vamos lá amigões, a gente já tá acabando o problema.
Pois bem, agora que temos todos os valores da forças podemos calcular o alongamento vertical em , porém, devemos descobrir alguns alongamentos antes que servirão de base para esse cálculo.
Passo 4
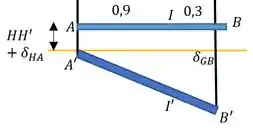
Agora é um momento chave ein: nessas questões a gente precisa se ligar na geometria do problema. Vamos desenhar, para ficar maneiro de visualizar. Todos os cabos sofrem tração, então alongam.
Primeiro, a gente quer achar o deslocamento final do ponto :
A gente pode usar semelhança de triângulos e escrever
Agora finalmente a gente consegue achar o deslocamento de , também por semelhança de triângulos:
