Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 27
Uma bola cujas extremidades foram truncadas é usada para suportar a carga de apoio Se o módulo de elasticidade para o material for , determine o decréscimo em sua altura quando a carga é aplicada.
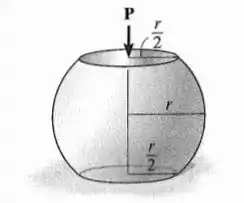
Passo 1
Queremos encontrar o decréscimo na altura da “bola” quando a carga for aplicada. Para esse caso vamos ter que o decréscimo vai ser dado por uma integral que pode ser calculada como sendo
Passo 2
Podemos fazer a seguinte construção geométrica para modelar esse problema
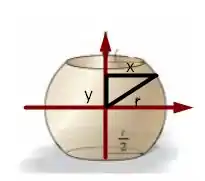
Aplicando Pitágoras no triângulo destacado na figura, vamos ter
Assim, vamos ter
Também podemos fazer o seguinte pitágora
Passo 3
Por fim, basta substituirmos os valores nas integrais e está resolvido o nosso problema
Resposta
Exercícios de Livros Relacionados
O corpo de prova representa um sistema de matriz reforçado por filamentos feitos de plástico (matriz) e vidro (fibra). Se houver n fibras, cada uma com área de seção transversal A f e módulo E f , emb
O carregamento distribuído é sustentado pelas três barras de suspensão. A B e E F são feitas de alumínio eC D é feita de aço. Se cada barra tiver área de seção transversal de 450mm 2 , determine a int
O elo rígido é sustentado por um pino em A , um cabo de aço B C com comprimento de 200mm quando não alongado com área de seção transversal de 22,5mm 2 e um bloco curto de alumínio com 50mm de comprime
As três barras de suspensão são feitas do mesmo material e têm áreas de seção transversal iguais, A . Determine a tensão normal média em cada barra se a viga rígida A C E for submetida à força P .
A barra está presa por um pino em A e é sustentada por duas hastes de alumínio, cada uma com diâmetro de 25mm e módulo de elasticidade E a l =70GPa . Considerando que a barra é rígida e inicialmente v