Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 110
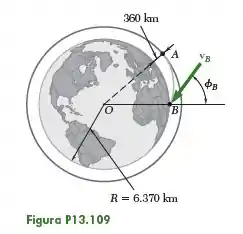
No Problema 13.109, a velocidade do veículo espacial foi diminuída quando ele passava por acionando seu motor em um sentido oposto ao do movimento. Uma estratégia alternativa para tirar o veículo espacial de sua órbita circular seria girá-lo de modo a que o motor apontasse para longe da Terra e, então, fornecer uma velocidade incremental em direção ao centro da Terra. Isso provavelmente exigiria um menor consumo de energia para acionar o motor em , mas poderia resultar em uma descida muito rápida para . Considerando o uso dessa estratégia com apenas 50% do consumo de energia do Problema 13.109, determine os valores resultantes de e .
Passo 1
Olá, pessoal! Tudo bem?
O problema pede que determinemos os valores resultantes de e , considerando o uso da estratégia de girar o veículo espacial de modo que o motor aponte para longe da Terra e, assim, forneça uma velocidade incremental em direção ao centro da Terra, isso considerando apenas 50% do consumo de energia do Problema 13.109. O enunciado e a figura nos fornecem as seguintes informações:
Em posse das altitudes dos pontos e e do raio da Terra, podemos calcular e :
Passo 2
Para a orbita circular de raio :
Sabemos que, pela 2ª Lei de Newton:
Conforme a Eq. 12.28:
Então,
Sabendo que, para um corpo em órbita circular,
Temos que,
Assim, sendo e :
O produto , pode ser expresso conforme a Eq. 12,29:
E sendo
Substituímos os valores na equação para obtermos :
Em posse de e de , podemos calcular:
Passo 3
Do Problema 13.109, sabemos que
Calculando temos,
Como o enunciado quer que consideremos apenas 50% do consumo de energia do Problema 13.109, temos:
Então, o incremento de energia cinética em é:
Passo 4
Calculando a energia cinética e potencial.
Ponto A:
Ponto B:
Passo 5
Em posse das energias cinética e potencial, vamos aplicar o princípio da conservação da energia:
Passo 6
E, aplicando a conservação do momento angular, encontramos :