Resolva o problema 14.8 utilizando a equação de conservação de energia.

Fala!

O enunciado nos dá as seguintes informações:

Comprimento não deformado da mola: ;

Comprimento da mola antes de acionar o gatilho:

Destendimento da mola:

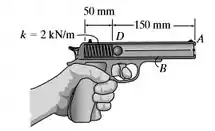
Constante elastica da mola: ;

Massa da bala:

Devemos determinar a velocidade da bala ao deixar a arma no ponto . A mola inicialmente está parada, a gente aperta o gatilho, ela distende um pouco. Esse movimento joga a bala para fora da arma.

Mas vamos determinar essa velocidade pela conservação de energia. Só repara que não vamos levar em conta a energia potencial gravitacional pois não temos variação de altura.

Vamos pensar no que está acontecendo. A bala, antes de acionar o gatilho, está paradinha encostada na mola. Então, quando o gatilho não está acionado, nossa bala tem apenas energia potencial elástica, já que ela está parada (não tem energia cinética):

Quando acionamos o gatilho, a mola estica . Isso quer dizer que a deformação dela fica

Como não há atrito, a velocidade que a bala tem desde o instante que ela deixa de encostar na mola vai ser a mesma que ela vai ter ao passar por . Então se a gente descobrir a velocidade nesse instante, a gente descobre .

No instante limite onde a bala está prestes a desencostar da mola, ela vai ter a energia cinética, porque ela já está em movimento e a potencial elástica porque ela ainda está encostada na mola. Então:

Pela conservação de energia:

A ideia é a gente usar essa equação para achar . Bora!