Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 94

Um recipiente de massa desprezível está ligado a duas molas idênticas de rigidez k= 250 N/m. Se uma caixa de 10 kg é solta de uma altura de 0,5 m acima do recipiente, determine o deslocamento vertical máximo d . Inicialmente, cada mola tem uma tração de 50   N.

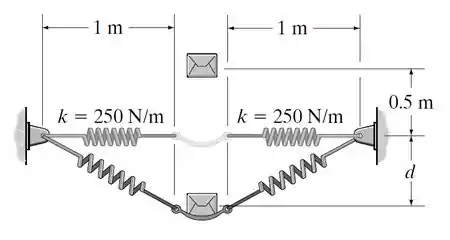
Passo 1

Primeiramente é necessário calcular as energias para as posições ( 1 ) e ( 2 ) . Com referência ao dado da imagem, a energia potencial gravitacional da caixa nas posições

Energia potencial:

( V g ) 1 = m g h 1 = 10 9,81 0 = 0  

E,

  ( V g ) 2 = m g h 2 = 10 9,81 - 0,5 + d = - 98,1 ( 0,5 + d )

Inicialmente a mola se estende

s 1 = F k k = 50 250 = 0,2

Assim, o comprimento da mola quando não está esticada é l 0 = 1 - 0.2 = 0,8   m e a energia pontecial elástica inicial de cada mola é

( V e ) 1 = 2 1 2 k s 1 2 = 2 250 2 0,2 2 = 10   J

Quando a caixa está na posição (2) a mola se estende

s 2 = ( d 2 + 1 2 - 0,8 ) m

A energia elástica potencial das molas quando a caixa está na posição é

( V e ) 2 = 2 1 2 k s 2 2 = 2 250 2 d 2 + 1 - 0,8 2 = 250 ( d 2 - 1,6 d 2 + 1 + 1,64 ) .

Passo 2

Conservação de energia:

T 1 + V 1 + T 2 + V 2

1 2 m v 1 2 + ( V g ) 1 + ( V e ) 1 = 1 2 m v 2 2 + V g 2 + V 2 2  

0 + 0 + 10 = 0 + - 98,1 0,5 + d + 250 ( d 2 - 1,6 d 2 + 1 + 1,64

250 d 2 - 98,1 d - 400 d 2 + 1 + 350,95 = 0

Resolvendo a equação acima.

d = 1,34   m

Resposta

O Deslocamento vertical máximo d para esse caso é de 1,34   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que os valores v A e v P da velocidade de um satélite da Terra no apogeu A e no perigeu P de uma órbita elíptica estão definidos pelas relações v A 2 = 2 G M r A + r P r P r Av P 2 = 2 G M r A
Usando as respostas obtidas no Problema 13.107, mostre que a órbita circular pretendida e a órbita elíptica resultante interceptam-se nas extremidades do eixo menor da órbita elíptica.
Quando o módulo lunar foi deixado à deriva após o retorno de dois dos astronautas da Apollo ao módulo de comando, que orbitava a Lua a uma altitude de 140k m , sua velocidade foi reduzida para deixá--
Sabendo que a velocidade de uma sonda espacial experimental lançada da Terra tem intensidade v A = 32,32 × 10 3k m / h no ponto A , determine a velocidade da sonda quando ela passar pelo ponto B .
Quanta energia por quilograma deve ser fornecida a um satélite a fim de colocá-lo em uma órbita circular a uma altitude de ( a ) 600 k m e ( b )6.000k m ?